Series and Parallel Circuits
Rules of Thumb for Series and Parallel Resistors
There are a few situations that may call for some creative resistor combinations. For example, if we’re trying to set up a very specific reference voltage you’ll almost always need a very specific ratio of resistors whose values are unlikely to be “standard” values. And while we can get a very high degree of precision in resistor values, we may not want to wait the X number of days it takes to ship something, or pay the price for non-stocked, non-standard values. So in a pinch, we can always build our own resistor values.
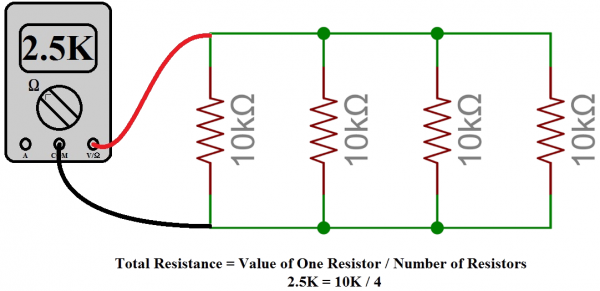
Tip #1: Equal Resistors in Parallel
Adding N like-valued resistors R in parallel gives us R/N ohms. Let’s say we need a 2.5kΩ resistor, but all we’ve got is a drawer full of 10kΩ's. Combining four of them in parallel gives us 10kΩ/4 = 2.5kΩ.
Tip #2: Tolerance
Know what kind of tolerance you can tolerate. For example, if you needed a 3.2kΩ resistor, you could put 3 10kΩ resistors in parallel. That would give you 3.3kΩ, which is about a 4% tolerance from the value you need. But, if the circuit you're building needs to be closer than 4% tolerance, we can measure our stash of 10kΩ’s to see which are lowest values because they have a tolerance, too. In theory, if the stash of 10kΩ resistors are all 1% tolerance, we can only get to 3.3kΩ. But part manufacturers are known to make just these sorts of mistakes, so it pays to poke around a bit.
Tip #3: Power Ratings in Series/Parallel
This sort of series and parallel combination of resistors works for power ratings, too. Let’s say that we need a 100Ω resistor rated for 2 watts (W), but all we’ve got is a bunch of 1kΩ quarter-watt (¼W) resistors (and it’s 3am, all the Mountain Dew is gone, and the coffee’s cold). You can combine 10 of the 1kΩ's to get 100Ω (1kΩ/10 = 100Ω), and the power rating will be 10x0.25W, or 2.5W. Not pretty, but it will get us through a final project, and might even get us extra points for being able to think on our feet.
We need to be a little more careful when we combine resistors of dissimilar values in parallel where total equivalent resistance and power ratings are concerned. It should be completely obvious to the reader, but...
Tip #4: Different Resistors in Parallel
The combined resistance of two resistors of different values is always less than the smallest value resistor. The reader would be amazed at how many times someone combines values in their head and arrives at a value that’s halfway between the two resistors (1kΩ || 10kΩ does NOT equal anything around 5kΩ!). The total parallel resistance will always be dragged closer to the lowest value resistor. Do yourself a favor and read tip #4 10 times over.
Tip #5: Power Dissipation in Parallel
The power dissipated in a parallel combination of dissimilar resistor values is not split evenly between the resistors because the currents are not equal. Using the previous example of (1kΩ || 10kΩ), we can see that the 1kΩ will be drawing 10X the current of the 10kΩ. Since Ohm’s Law says power = voltage x current, it follows that the 1kΩ resistor will dissipate 10X the power of the 10kΩ.
Ultimately, the lessons of tips 4 and 5 are that we have to pay closer attention to what we’re doing when combining resistors of dissimilar values in parallel. But tips 1 and 3 offer some handy shortcuts when the values are the same.