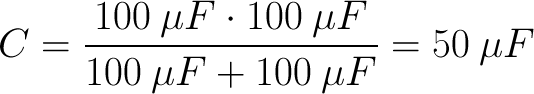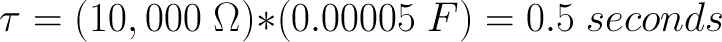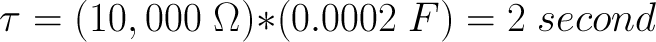Series and Parallel Circuits

Contributors: Pete-O

Experiment Time - Part 3, Even More...

Now we’re on to the interesting parts, starting with connecting two capacitors in series. Remember that we said the result of which would be similar to connecting two resistors in parallel. If this is true, we can expect (using product-over-sum)

What’s that going to do to our time constant?

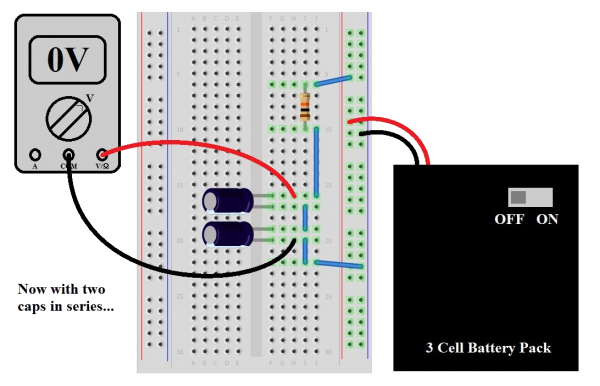
With that in mind, plug in another capacitor in series with the first, make sure the meter is reading zero volts (or there-abouts) and flip the switch to “ON”. Did it take about half as much time to charge up to the battery pack voltage? That’s because there’s half as much capacitance. The electron gas tank got smaller, so it takes less time to charge it up. A third capacitor is suggested for this experiment just to prove the point, but we’re betting the reader can see the writing on the wall.

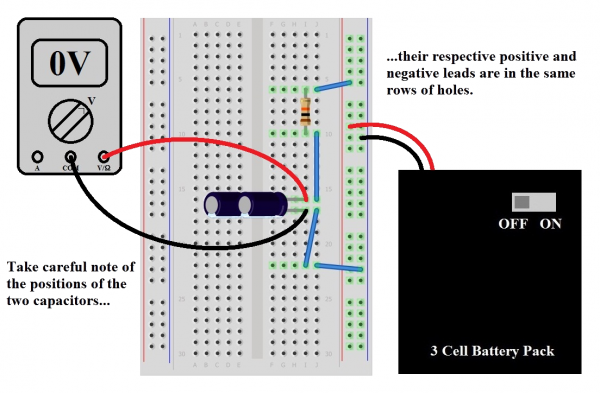
Now we’ll try capacitors in parallel, remembering that we said earlier that this would be like adding resistors in series. If that’s true, then we can expect 200µF, right? Then our time constant becomes

This means that it will now take about 10 seconds to see the parallel capacitors charge up to the supply voltage of 4.5V.

For the proof, start with our original circuit of one 10kΩ resistor and one 100µF capacitor in series, as hooked up in the first diagram for this experiment. We already know that the capacitor is going to charge up in about 5 seconds. Now add a second capacitor in parallel. Make sure the meter is reading close to zero volts (discharge through a resistor if it isn't reading zero), and flip the switch on the battery pack to “ON”. Takes a long time, doesn't it? Sure enough, we made the electron gas tank bigger and now it takes longer to fill it up. To prove it to yourself, try adding the third 100µF capacitor, and watch it charge for a good, long time.