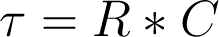Series and Parallel Circuits
Experiment Time - Part 3
What you'll need:
- One 10kΩ resistor
- Three 100µF caps
- A 3-cell AA battery holder
- Three AA cells
- A breadboard
- A multimeter
- Clip-leads
Let’s see some series and parallel connected capacitors in action. This will be a little trickier than the resistor examples, because it’s harder to measure capacitance directly with a multimeter.
Let’s first talk about what happens when a capacitor charges up from zero volts. When current starts to go in one of the leads, an equal amount of current comes out the other. And if there’s no resistance in series with the capacitor, it can be quite a lot of current. In any case, the current flows until the capacitor starts to charge up to the value of the applied voltage, more slowly trickling off until the voltages are equal, when the current flow stops entirely.
As stated above, the current draw can be quite large if there’s no resistance in series with the capacitor, and the time to charge can be very short (like milliseconds or less). For this experiment, we want to be able to watch a capacitor charge up, so we’re going to use a 10kΩ resistor in series to slow the action down to a point where we can see it easily. But first we need to talk about what an RC time constant is.
What the above equation says is that one time constant in seconds (called tau) is equal to the resistance in ohms times the capacitance in farads. Simple? No? We shall demonstrate on the next page.