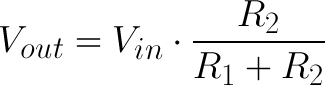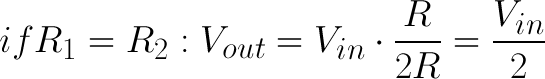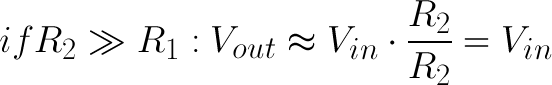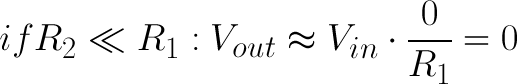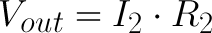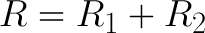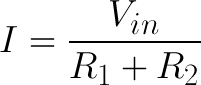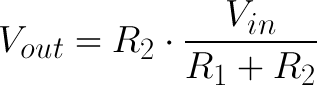Voltage Dividers
Introduction
A voltage divider is a simple circuit which turns a large voltage into a smaller one. Using just two series resistors and an input voltage, we can create an output voltage that is a fraction of the input. Voltage dividers are one of the most fundamental circuits in electronics. If learning Ohm's law was like being introduced to the ABC's, learning about voltage dividers would be like learning how to spell cat.
These are examples of potentiometers - variable resistors which can be used to create an adjustable voltage divider. We'll learn more about these soon.
Covered in this Tutorial
- What a voltage divider circuit looks like.
- How the output voltage depends on the input voltage and divider resistors.
- How voltage dividers behave in the real-world.
- Real-life voltage divider applications.
Suggested Reading
This tutorial builds on basic electronics knowledge. If you haven't already, consider reading these tutorials:
Ideal Voltage Divider
There are two important parts to the voltage divider: the circuit and the equation.
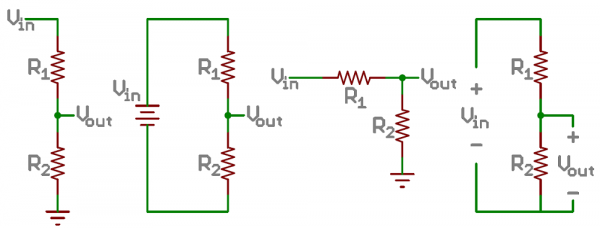
The Circuit
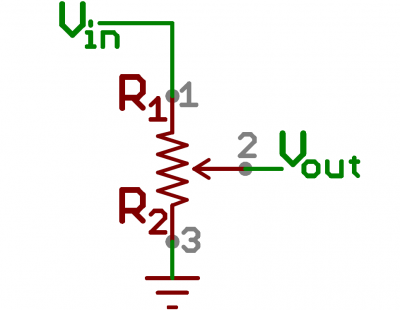
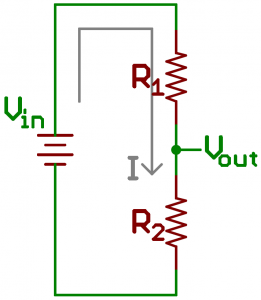
A voltage divider involves applying a voltage source across a series of two resistors. You may see it drawn a few different ways, but they should always essentially be the same circuit.
We'll call the resistor closest to the input voltage (Vin) R1, and the resistor closest to ground R2. The voltage drop across R2 is called Vout, that's the divided voltage our circuit exists to make.
That's all there is to the circuit! Vout is our divided voltage. That's what'll end up being a fraction of the input voltage.
The Equation
The voltage divider equation assumes that you know three values of the above circuit: the input voltage (Vin), and both resistor values (R1 and R2). Given those values, we can use this equation to find the output voltage (Vout):
This equation states that the output voltage is directly proportional to the input voltage and the ratio of R1 and R2. If you'd like to find out where this comes from, check out this section where the equation is derived. But for now, just write it down and remember it!
Calculator
Have some fun experimenting with inputs and outputs to the voltage divider equation! Below, you can plug in numbers for Vin and both resistors and see what kind of output voltage they produce.
Or, if you adjust Vout, you'll see what resistance value at R2 is required (given a Vin and R1).
Simplifications
There are a few generalizations that are good to keep in mind when using voltage dividers. These are simplifications that make evaluating a voltage dividing circuit just a little easier.
First, if R2 and R1 are equal then the output voltage is half that of the input. This is true regardless of the resistors' values.
If R2 is much larger (at least an order of magnitude) than R1, then the output voltage will be very close to the input. There will be very little voltage across R1.
Conversely, if R2 is much smaller than R1, the output voltage will be tiny compared to the input. Most of the input voltage will be across R1
Applications
Voltage dividers have tons of applications, they are among the most common of circuits electrical engineers use. Here are just a few of the many places you'll find voltage dividers.
Potentiometers
A potentiometer is a variable resistor which can be used to create an adjustable voltage divider.
Internal to the pot is a single resistor and a wiper, which cuts the resistor in two and moves to adjust the ratio between both halves. Externally there are usually three pins: two pins connect to each end of the resistor, while the third connects to the pot's wiper.
If the outside pins connect to a voltage source (one to ground, the other to Vin), the output (Vout at the middle pin will mimic a voltage divider. Turn the pot all the way in one direction, and the voltage may be zero; turned to the other side the output voltage approaches the input; a wiper in the middle position means the output voltage will be half of the input.
Potentiometers come in a variety of packages, and have many applications of their own. They may be used to create a reference voltage, adjust radio stations, measure position on a joystick, or in tons of other applications which require a variable input voltage.
Reading Resistive Sensors
Many sensors in the real world are simple resistive devices. A photocell is a variable resistor, which produces a resistance proportional to the amount of light it senses. Other devices like flex sensors, force-sensitive resistors, and thermistors, are also variable resistors.
It turns out voltage is really easy for microcontrollers (those with analog-to-digital converters - ADC’s - at least) to measure. Resistance? Not so much. But, by adding another resistor to the resistive sensors, we can create a voltage divider. Once the output of the voltage divider is known, we can go back and calculate the resistance of the sensor.
For example, the photocell's resistance varies between 1kΩ in the light and about 10kΩ in the dark. If we combine that with a static resistance somewhere in the middle - say 5.6kΩ, we can get a wide range out of the voltage divider they create.
| Light Level | R2 (Sensor) | R1 (Fixed) | Ratio R2/(R1+R2) | Vout |
| Light | 1kΩ | 5.6kΩ | 0.15 | 0.76 V |
| Dim | 7kΩ | 5.6kΩ | 0.56 | 2.78 V |
| Dark | 10kΩ | 5.6kΩ | 0.67 | 3.21 V |
A swing of about 2.45V from light to dark. Plenty of resolution for most ADCs!
Level Shifting
More complicated sensors may transmit their readings using heavier serial interfaces, like a UART, SPI, or I2C. Many of those sensors operate at a relatively low voltage, in order to conserve power. Unfortunately, it's not uncommon that those low-voltage sensors are ultimately interfacing with a microcontroller operating at a higher system voltage. This leads to a problem of level shifting, which has a number of solutions including voltage dividing.
For example, an ADXL345 accelerometer allows for a maximum input voltage of 3.3V, so if you try to interface it with an Arduino (assume operating at 5V), something will need to be done to step down that 5V signal to 3.3V. Voltage divider! All that's needed is a couple resistors whose ratio will divide a 5V signal to about 3.3V. Resistors in the 1kΩ-10kΩ range are usually best for such an application; let's
Keep in mind, this solution only works in one direction. A voltage divider alone will never be able to step a lower voltage up to a higher one.
Application Dont's
As tempting as it may be to use a voltage divider to step down, say, a 12V power supply to 5V, voltage dividers should not be used to supply power to a load.
Any current that the load requires is also going to have to run through R1. The current and voltage across R1 produce power, which is dissipated in the form of heat. If that power exceeds the rating of the resistor (usually between ⅛W and 1W), the heat begins to become a major problem, potentially melting the poor resistor.
That doesn't even mention how inefficient a voltage-divider-power-supply would be. Basically, don't use a voltage divider as a voltage supply for anything that requires even a modest amount of power. If you need to drop down a voltage to use it as a power supply, look into voltage regulators or switching supplies.
Extra Credit: Proof
If you haven't yet gotten your fill of voltage dividers, in this section we'll evaluate how Ohm's law is applied to produce the voltage divider equation. This is a fun exercise, but not super-important to understanding what voltage dividers do. If you're interested, prepare for some fun times with Ohm's law and algebra.
Evaluating the circuit
So, what if you wanted to measure the voltage at Vout? How could Ohm's law be applied to create a formula to calculate the voltage there? Let's assume that we know the values of Vin, R1, and R2, so let's get our Vout equation in terms of those values.
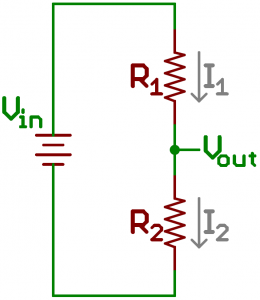
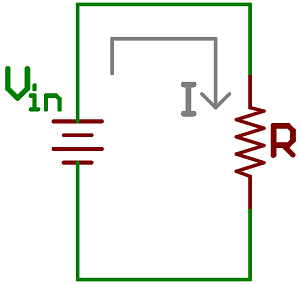
Let's start by drawing out the currents in the circuit--I1 and I2--which we'll call the currents across the respective resistors.
Our goal is to calculate Vout, what if we applied Ohm's law to that voltage? Easy enough, there's just one resistor and one current involved:
Sweet! We know R2's value, but what about I2? That's an unknown value, but we do know a little something about it. We can assume (and this turns out to be a big assumption) that I1 is equivalent to I2. Alright, but does that help us? Hold that thought. Our circuit now looks like this, where I equals both I1 and I2.
What do we know about Vin? Well, Vin is the voltage across both resistors R1 and R2. Those resistors are in series. Series resistors add up to one value, so we could say:
And, for a moment, we can simplify the circuit to:
Ohm's law at its most basic! Vin = I * R. Which, if we turn that R back into R1 + R2, can also be written as:
And since I is equivalent to I2, plug that into our Vout equation to get:
And that, my friends, is the voltage divider equation! The output voltage is a fraction of the input voltage, and that fraction is R2 divided by the sum of R1 and R2.
Interested in learning more foundational topics?
See our Engineering Essentials page for a full list of cornerstone topics surrounding electrical engineering.
Resources and Going Further
Now that you've got the gist of one of the most common circuits in electronics, there's a world of new stuff to learn!
Would you like to learn how a microcontroller, like an Arduino, could read the analog voltage produced by a voltage divider?
With the power of the voltage divider and the ADC, you can accomplish a lot in the world of electronics. Check out these other great tutorials.
- Some varieties of accelerometers and gyroscopes have anlog outputs that must be read in on an ADC to get usable values.
- Pulse-width Modulation (PWM) is like an analog output, which is the opposite of analog input.
- The INA169 allows you to sense current using ADC.
- Using a voltage divider and the ADC, you can read in all sorts of sensors and variable components such as trimpots, joysticks, sliders, and force sensitive resistors amongst many, many more.
- The Arduino map() function
- Arduino Analog Pins
- The Uh-Oh Battery Indicator Hookup Guide uses a voltage divider to tell you if your battery is getting too low.