LogicBlocks Experiment Guide
9. XOR Gate
Up till now, you've been happily living in a world with just three fundamental logic gates. It's time to shatter that perception! Prepare for the revelation that is...the exclusive OR.
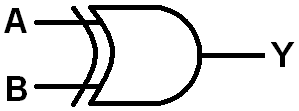
An exclusive OR, shortened to XOR, is similar to an OR gate with one major difference. Can you tell from the truth table?:
| Input A | Input B | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
When we say exclusive, we mean it. An XOR only produces a 1 when a lone input is also 1. If two or more inputs are 1, the XOR gate outputs a 0.
It turns out the XOR gate is an incredibly useful function in digital logic. So useful, in fact, that it gets its own circuit symbol -- kind of a modified OR gate, with a concave line preceding the gate we're used to:
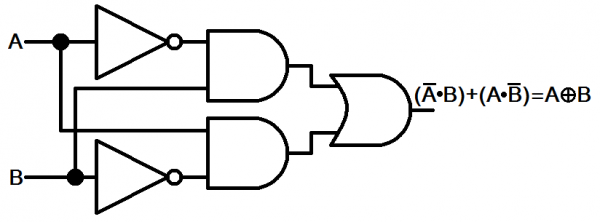
Like all of the previous experiments, the XOR gate can be implemented with the three fundamental digital logic gates. A mix of NOTs, ANDs, and an OR:
Let's LogicBlock it!
What You'll Need
- 2x AND Blocks
- 1x OR Block
- 2x NOT Blocks
- 2x Input Blocks
- 2x Splitter Blocks
- 1x Power Block
- 1x Feedback cable
LogicBlocks Layout
Construct the XOR as shown below:
The output of the XOR LogicBlocks circuit is represented by the yellow LED on the final OR gate.
The Experiment
Prove the XOR truth table true by toggling both inputs. The LED on the OR block should only light up when you have one or the other of the inputs on.
- Is the XOR a combinational or sequential circuit?
- Can you think of a real life example where a statement is true if only one of the inputs is also true?
Sub-Experiments
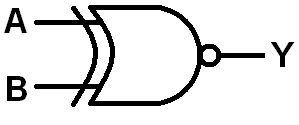
Remember NAND and NOR? Well XOR has it's own complement...XNOR. Like the other two negative gates, XNOR has its own bubbled circuit diagram:
The truth table for the 2-input XNOR looks like this:
| Input A | Input B | Output |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
What's really neat about the XNOR is it only proves true when both inputs are the same. That's why we call this operator the logical equality. You could even use the equals sign (=) as the XNOR operator. The equality operator is used all over electronics and programming. If you ever need to check if two statements are equal, an XNOR will be involved.
Hey we've got another NOT Block lying around, let's make an XNOR LogicBlocks circuit! Replace the Power Block with a NOT Block, and plug the Power Block into the end of that.
The output of this circuit is represented by the red LED on the final NOT Block.
- Try toggling both Input Blocks. Does the output LED only illuminate when they're both equal?