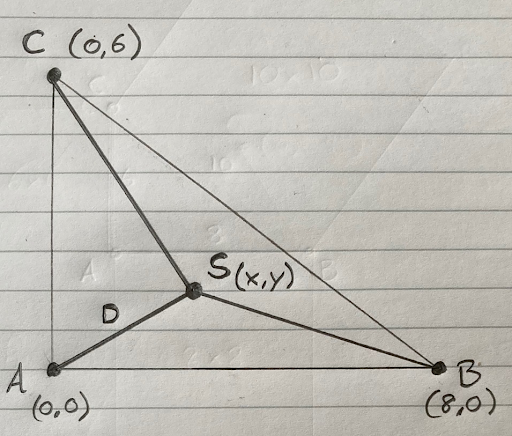Sound Location Part 2 with the Qwiic Sound Trigger and the u-blox ZED-F9x

Contributors: PaulZC

Sound Source Triangulation

Last time, we learned that we can calculate the location of a sound by measuring the difference in the sound’s time-of-arrival at two sound triggers. In our 1D example, we:

• Converted the time difference into distance (by multiplying by the speed of sound)
• Subtracted that distance from the distance between our two sound triggers
• And then divided by 2 to calculate the distance from the closest trigger (the one that detects the sound first)

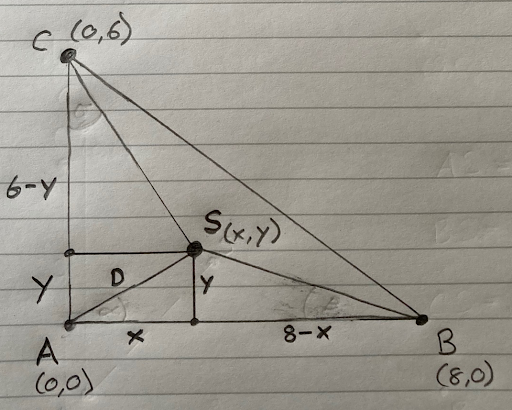
In 2D, there is a little more math involved. Let’s call our three sound trigger systems A, B and C. A is our reference or origin. If we position trigger B due East from A, we can call the line that joins A to B our X axis. Remember when you used to draw graphs in math class? You had the origin in the bottom left corner of your graph paper and you drew the X axis horizontally out to the right. We are doing the same thing here. Trigger A is our origin at X = 0 and Y = 0. We write that as (0,0). If Trigger B is 8 metres (8m) away from A, then its location is X = 8 and Y = 0. We write that as (8,0).

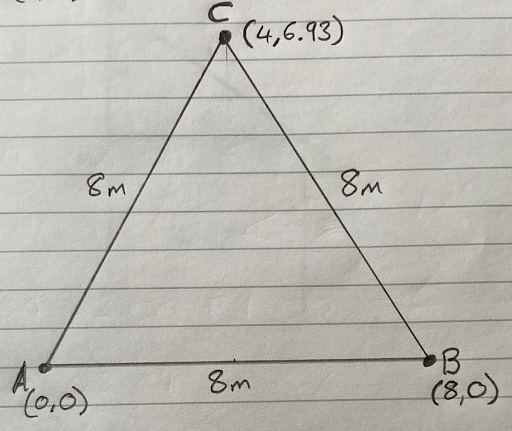
So far, so good. Now, where should we position trigger C? In reality, it doesn’t really matter. We could position C so that ABC forms a perfect equilateral triangle (a triangle where all three sides are the same length). That would give us the best coverage of the area. But the coordinates of C would be (4,6.93). Not pleasant.

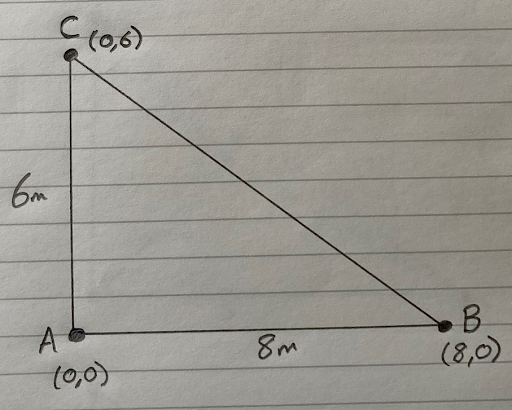
To keep the math simpler for this example, let’s position C 6m due North from A. The coordinates of C are X = 0 and Y = 6. We write that as (0,6).

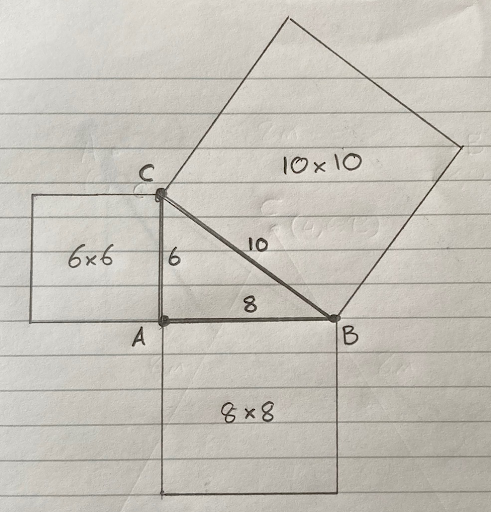
We know the distance from A to B is 8m, and that the distance from A to C is 6m. But what about the distance from B to C? We need to know that too. If we get out a tape measure and measure it, we’ll find it is exactly 10m. If you remember Pythagoras’ Theorem from your math class, the square on the hypotenuse is equal to the sum of the squares on the other two sides, we can calculate the distance from B to C by:

• Squaring (multiplying by itself) the distance from A to B: 8 x 8 = 64
• Squaring (multiplying by itself) the distance from A to C: 6 x 6 = 36
• Summing (adding) them: 64 + 36 = 100
• Calculating the square root: √100 = 10

Again, to keep the math easier, let’s pretend that the speed of sound is 1 metre per second (1m/s), not 343.42m/s.

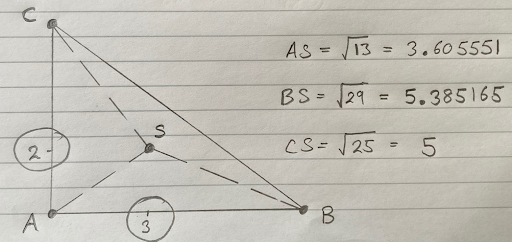
Now, let’s suppose our sound trigger system is running and it detects a sound:

• The time recorded by trigger A is 10:00:03.605551
• The time recorded by trigger B is 10:00:05.385165
• The time recorded by trigger C is 10:00:05.000000

Let’s calculate the differences in those times:

• A records the sound first, so we will use that as our reference
• B records the sound 10:00:05.385165 - 10:00:03.605551 = 1.779614 seconds later
• C records the sound 10:00:05.000000 - 10:00:03.605551 = 1.394449 seconds later

With the speed of sound being 1m/s, we now know that the sound travelled an extra 1.779614m when travelling to B compared to A. And we know that the sound travelled an extra 1.394449m when travelling to C compared to A.

What we do not know is how far the sound travelled to get to A. That’s the first thing we need to calculate.

Let’s call the location of the sound: S. Let’s call the coordinates of S: ( x , y ). Let’s call the distance from S to A: D.

If we sketch that - not to scale - it looks like this:

We know that:

• The distance from S to A is D metres
• The distance from S to B is D + 1.779614 metres
• The distance from S to C is D + 1.394449 metres

In order to find the location of S, we need to use triangles. That’s why this technique is called “triangulation”. In trigonometry and geometry, triangulation is the process of determining the location of a point by forming triangles to it from known points.

If we divide our diagram up into more triangles:

We can use Pythagoras’ Theorem to calculate the distances we need:

• D² = x² + y²
• (D + 1.779614)² = (8 - x)² + y²
• (D + 1.394449)² = x² + (6 - y)²

We can write that as:

• D² = x² + y²
• y² = (D + 1.779614)² - (8 - x)²
• x² = (D + 1.394449)² - (6 - y)²

We need to solve for D. To begin, let’s substitute the value for y² from the second equation into the first equation:

• D² = x² + (D + 1.779614)² - (8 - x)²

Multiplying out the brackets, that becomes:

• D² = x² + D² + 1.779614.D + 1.779614.D + 1.779614² - ( 8² - 8x - 8x + x² )

Simplifying, it becomes:

• D² = x² + D² + 3.559228.D + 3.167026 - (64 - 16.x + x²)

If we remove the brackets:

• D² = x² + D² + 3.559228.D + 3.167026 - 64 + 16.x - x²

The D² cancel out and so do the x² leaving:

• 0 = 3.559228.D + 3.167026 - 64 + 16.x

One final rearrange leaves:

• 16.x = -3.559228.D + 60.832974

If we divide through by 16 we are left with:

• x = -0.222452.D + 3.802061

Now let’s go back to our three triangles:

• D² = x² + y²
• y² = (D + 1.779614)² - (8 - x)²
• x² = (D + 1.394449)² - (6 - y)²

This time, let’s substitute the value for x² from the third equation into the first equation:

• D² = (D + 1.394449)² - (6 - y)² + y²

Multiplying out the brackets, that becomes:

• D² = D² + 1.394449D + 1.394449D + 1.944488 - (36 - 6y - 6y + y²) + y²

If we remove the brackets:

• D² = D² + 1.394449D + 1.394449D + 1.944488 - 36 + 6y + 6y - y² + y²

Again, the D² cancel out and so do the y² leaving:

• 0 = 2.788898.D + 1.944488 - 36 + 12.y

One final rearrange leaves:

• 12.y = -2.788898.D + 34.055512

If we divide through by 12 we are left with:

• y = -0.232408.D + 2.837959

Now we can put our values for x and y back into our first equation:

• D² = x² + y²

• D² = (-0.222452.D + 3.802061)² + (-0.232408.D + 2.837959)²

Multiplying out the brackets, we get:

• D² = 0.049485.D² - 1.691552.D + 14.455668 + 0.054013.D² - 1.319129.D + 8.054011

Simplifying:

• 0.896502.D² + 3.010681.D - 22.509679 = 0

Now, I’m sure you will remember quadratic equations from your math class too? We can solve for D using the equation:

• ( -b +/- √(b² - 4.a.c ) ) / 2.a

• a = 0.896502

• b = 3.010681
• c = -22.509679

Inserting our values, D is:

• ( -3.010681 +/- √(9.064200 + 80.719889) ) / 1.793004

Which equals:

• 3.605550 or -6.963804

We can ignore the negative value since it is not within our triangle. Now we know that D is 3.605550m !

Looking back at our equations for x and y:

• x = -0.222452.D + 3.802061
• y = -0.232408.D + 2.837959

If we insert the value for D, we can finally calculate the x and y coordinates of S:

• ( -0.802062 + 3.802061 , -0.837959 + 2.837959 )

Which is:

• ( 3.000 , 2.000 )

Fancy that!

This technique can be used on any configuration of trigger locations. They don’t have to be positioned in a neat right angle triangle. If you would like proof of that and would like to see the math to solve it, have a look at the section called Here There Be Dragons!