Lessons in Algorithms

Contributors: Nate, barryjh

Build a little, Test a little, Learn a lot

While everyone’s brain works a little differently, I suggest that you try an iterative strategy, especially when you are solving a problem that does not have a clearly defined methodology going into it. I also suggest that when you feel you are ready to make a major tweak to an algorithm, you make a copy of the algorithm before starting to modify the copy, or start with an empty function and start pulling in pieces of the previous iteration. You can use source control to preserve your previous iteration, but I like having the previous iteration(s) in the code so I can easily reference it when working on the next iteration. I usually don’t like to write more than 10 or 20 lines of code without at minimum verifying it complies, but I really want to run it and print something out as confirmation that my logic and assumptions are correct. I’ve done this my entire career and will usually complain if I don’t have target hardware available to actually run what I’m coding. Around 2006, I heard a saying from a former Rear Admiral:

I really identify with that statement, as it succinctly states why I always want to keep running and testing what I’m writing. It either allows you to confirm your assumptions or reveals you are heading down the wrong path, allowing you to quickly get on the right path without throwing away a lot of work. This was yet another reason that I chose Java as my prototype platform, as I could quickly start running and testing code plus graph it out visually, in spite of not having the actual speed bag hardware.

Additionally, you will see in the middle of all six runFx() functions there is code that keeps track of the current time in milliseconds and verifies that the time stamp delta in milliseconds has elapsed or it sleeps for 1 millisecond. This allowed me to watch the data scroll by in my Java plotting window and see how the filtering output looks. I passed in X, Y and Z acceleration data along with an X, Y and Z average value. Since I only used Z data in most algorithms, I started cheating and sending in other values to be plotted, so it’s a little confusing when looking at the graphs of one through five since they don’t match the legend. However, plotting in real time allowed me to see the data and watch the hit counter increment. I could actually see and feel a sense of the rhythm into which the punches were settling and how the acceleration data was being affected by the resonance at prolonged constant rhythm. In addition to the visual output using the Java System.out.println() function, I can output data to a window in the NetBeans IDE.

If you look in the Java subdirectory in my GitHub repository, there is a file named MainLoop.java. In that file, I have a few functions named run1() through run6(). These were my six major iterations of the speed bag algorithm code.

Here are some highlights for each of the six iterations.

runF1

runF1() used only the Z axis, and employed weak bias removal using a sliding window and fixed amplification of the filtered Z data. I created an element called delay, which is a way to delay input data so it could be aligned later with output of averaged results. This allowed the sliding window average to be subtracted from Z axis data based on surrounding values, not by previous values. Punch detection used straight comparison of amplified filter data being greater than average of five samples with a minimum of 250 milliseconds between detections.

runF2

runF2() used only Z axis, and employed weak bias removal via a sliding window but added dynamic beta amplification of the filtered Z data based on the average amplitude above the bias that was removed when the last punch was detected. Also, a dynamic minimum time between punches of 225ms to 270ms was calculated based on delta time since last punch was detected. I called the amount of bias removed noise floor. I added a button to stop and resume the simulation so I could examine the debug output and the waveforms. This allowed me to see the beta amplification being used as the simulation went along.

runF3

runF3() used X and Z axis data. My theory was that there might be a jolt of movement from the punching action that could be additive to the Z axis data to help pinpoint the actual punch. It was basically the same algorithm as RunF2 but added in the X axis. It actually worked pretty well, and I thought I might be onto something here by correlating X movement and Z. I tried various tweaks and gyrations as you can see in the code lots of commented out experiments. I started playing around with what I call a compressor, which took the sum of five samples to see if it would detect bunches of energy around when punches occur. I didn’t use it in the algorithm but printed out how many times it crossed a threshold to see if it had any potential as a filtering element. In the end, this algorithm started to implode on itself, and it was time to take what I learned and start a new algorithm.

runF4

In runF4(), I increased the bias removal average to 50 samples. It started to work in attenuation and sample compression along with a fixed point LSB to preserve some decimal precision to the integer attenuate data. Since one of the requirements was this should be able to run on 8-bit microcontrollers, I wanted to avoid using floating point and time consuming math functions in the final C/C++ code. I’ll speak more to this in the components section, but, for now, know that I’m starting to work this in. I’ve convinced myself that finding bursts of acceleration is the way to go. At this point, I am removing the bias from both Z and X axis then squaring. I then attenuate each, adding the results together but scaling X axis value by 10. I added a second stage of averaging 11 filtered values to start smoothing the bursts of acceleration. Next, when the smoothed value gets above a fixed threshold of 100, the unsmoothed combination of Z and X squared starts getting loaded into the compressor until 100 samples have been added. If the compressor output of the 100 samples is greater than 5000, it is recorded as a hit. A variable time between punches gate is employed, but it is much smaller since the compressor is using 100 samples to encapsulate the punch detection. This lowers the gate time to between 125 and 275 milliseconds. While showing some promise, it was still too sensitive. While one data set would be spot on another would be off by 10 or more punches. After many tweaks and experiments, this algorithm began to implode on itself, and it was once again time to take what I’ve learned and start anew. I should mention that at this tim I’m starting to think there might not be a satisfactory solution to this problem. The resonant vibrations that seem to be out of phase with the contacts of the bag just seems to wreak havoc on the acceleration seen when the boxer gets into a good rhythm. Could this all just be a waste of time?

runF5

runF5()'s algorithm started out with the notion that a more formal high pass filter needed to be introduced rather than an average subtracted from the signal. The basic premise of the high pass filter was to use 99% of the value of new samples added to 1% of the value of average. An important concept added towards the end of runF5’s evolution was to try to simplify the algorithm by removing the first stage of processing into its own file to isolate it from later stages. Divide and Conquer; it’s been around forever, and it really holds true time and time again. I tried many experiments as you can see from the many commented out lines in the algorithm and in the FrontEndProcessorOld.java file. In the end, it was time to carry forward the new Front End Processor concept and start anew with divide and conquer and a need for a more formal high pass filter.

runF6

With time running out, it's time to pull together all that has been learned up to now, get the Java code ready to port to C/C++ and implement real filters as opposed to using running averages. In runF6(), I had been pulling together the theory that I need to filter out the bias on the front end with a high pass filter and then try to use a low pass filter on the remaining signal to find bursts of acceleration that occur at a 2 to 4 Hertz frequency. No way was I going to learn how to calculate my own filter tap values to implement the high and low pass filters in the small amount of time left before the deadline. Luckily, I discovered the t-filter web site. Talk about a triple play. Not only was I able to put in my parameters and get filter tap values, I was also able to leverage the C code it generated with a few tweaks in my Java code. Plus, it converted the tap values to fixed point for me! Fully employing the divide and conquer concept, this final version of the algorithm introduced isolated sub algorithms for both Front End Processor and Detection Processing. This allowed me to isolate the two functions from each other except for the output signal of one becoming the input to the other, which enabled me to focus easily on the task at hand rather than sift through a large group of variables where some might be shared between the two stages.

With this division of responsibility, it is now easy to focus on making the clear task of the Front End Processor to remove the bias values and output at a level that is readily acceptable for input into the Detection Processor. Now the Detection processor can clearly focus on filtering and implementing a state machine that can pick out the punch events that should occur between 2 and 4 times per second.

One thing to note is that this final algorithm is much smaller and simpler than some of the previous algorithms. Even though its software, at some point in the process you should still do a technique called Muntzing. Muntzing is a technique to go back and look at what can be removed without breaking the functionality. Every line of code that is removed is one less line of code that can have a bug. You can Google Earl “Madman” Muntz to get a better understanding and feel for the spirit of Muntzing.

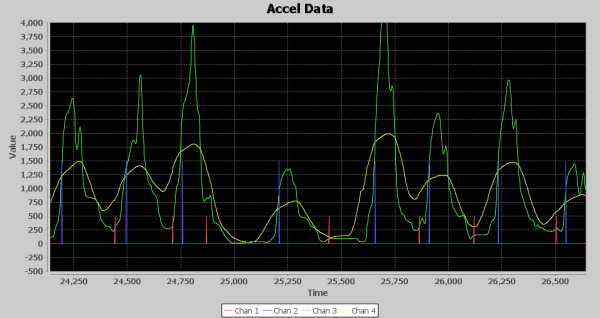
Above is the visual output from runF6. The Green line is 45 samples delayed of the output of the low pass filter, and the yellow line is an average of 99 values of the output of the low pass filter. The Detection Processor includes a detection algorithm that detects punches by tracking min and max crossings of the Green signal using the Yellow signal as a template for dynamic thresholding. Each minimum is a Red spike, and each maximum is a Blue spike, which is also a punch detection. The timescale is in milliseconds. Notice there are about three blue spikes per second inside the 2 to 4Hz range predicted. And the rest is history!