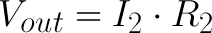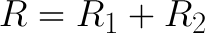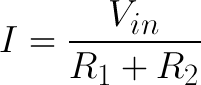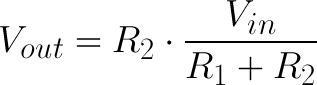Voltage Dividers

Contributors: jimblom

Extra Credit: Proof

If you haven't yet gotten your fill of voltage dividers, in this section we'll evaluate how Ohm's law is applied to produce the voltage divider equation. This is a fun exercise, but not super-important to understanding what voltage dividers do. If you're interested, prepare for some fun times with Ohm's law and algebra.

Evaluating the circuit

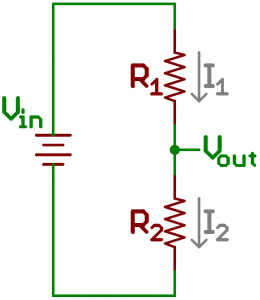
So, what if you wanted to measure the voltage at V_out? How could Ohm's law be applied to create a formula to calculate the voltage there? Let's assume that we know the values of V_in, R₁, and R₂, so let's get our V_out equation in terms of those values.

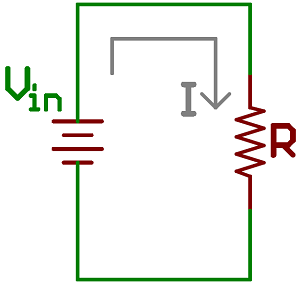
Let's start by drawing out the currents in the circuit--I₁ and I₂--which we'll call the currents across the respective resistors.

Our goal is to calculate V_out, what if we applied Ohm's law to that voltage? Easy enough, there's just one resistor and one current involved:

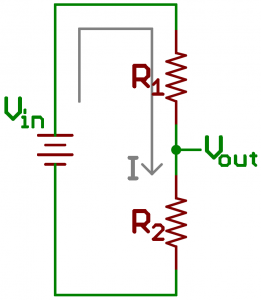
Sweet! We know R₂'s value, but what about I₂? That's an unknown value, but we do know a little something about it. We can assume (and this turns out to be a big assumption) that I₁ is equivalent to I₂. Alright, but does that help us? Hold that thought. Our circuit now looks like this, where I equals both I₁ and I₂.

What do we know about V_in? Well, V_in is the voltage across both resistors R₁ and R₂. Those resistors are in series. Series resistors add up to one value, so we could say:

And, for a moment, we can simplify the circuit to:

Ohm's law at its most basic! V_in = I * R. Which, if we turn that R back into R₁ + R₂, can also be written as:

And since I is equivalent to I₂, plug that into our V_out equation to get:

And that, my friends, is the voltage divider equation! The output voltage is a fraction of the input voltage, and that fraction is R₂ divided by the sum of R₁ and R₂.

Interested in learning more foundational topics?

See our Engineering Essentials page for a full list of cornerstone topics surrounding electrical engineering.

Take me there!