Light-Emitting Diodes (LEDs)
Delving Deeper
So you've graduated from LEDs 101 and you want more? Oh, don't worry, we've got more. Let's start with the science behind what makes LEDs tick... err... blink. We've already mentioned that LEDs are a special kind of diode, but let's delve a little deeper into exactly what that means:
What we call an LED is really the LED and the packaging together, but the LED itself is actually tiny! It's a chip of semiconductor material that's doped with impurities which creates a boundary for charge carriers. When current flows into the semi-conductor, it jumps from one side of this boundary to the other, releasing energy in the process. In most diodes that energy leaves as heat, but in LEDs that energy is dissipated as light!
The wavelength of light, and therefore the color, depends on the type of semiconductor material used to make the diode. That's because the energy band structure of semiconductors differs between materials, so photons are emitted with differing frequencies. Here's a table of common LED semiconductors by frequency:
While the wavelength of the light depends on the band gap of the semiconductor, the intensity depends on the amount of power being pushed through the diode. We talked about luminous intensity a little bit in a previous section, but there's more to it than just putting a number on how bright something looks.
The unit for measuring luminous intensity is called the candela, although when you're talking about the intensity of a single LED you're usually in the millicandela range. The interesting thing about this unit is that it isn't really a measure of the amount of light energy, but an actual measure of "brightness". This is achieved by taking the power emitted in a particular direction and weighting that number by the luminosity function of the light. The human eye is more sensitive to some wavelengths of light than others, and the luminosity function is a standardized model that accounts for that sensitivity.
The luminous intesity of LEDs can range from the tens to the tens-of-thousands of millicandela. The power light on your TV is probably about 100 mcd, whereas a good flashlight might be 20,000 mcd. Looking straight into anything brighter than a few thousand millicandela can be painful; don't try it.
Forward Voltage Drop
Oh, I also promised that we'd talk about the concept of Forward Voltage Drop. Remember when we were looking at the datasheet and I mentioned that the Forward Voltage of all of your LEDs added together can't exceed your system voltage? This is because every component in your circuit has to share the voltage, and the amount of voltage that every part uses together will always equal the amount that's available. This is called Kirchhoff's Voltage Law. So if you have a 5V power supply and each of your LEDs have a forward voltage drop of 2.4V then you can't power more than two at a time.
Kirchhoff's Laws also come in handy when you want to approximate the voltage across a given part based on the Forward Voltage of other parts. For instance, in the example I just gave there's a 5V supply and 2 LEDs with a 2.4V Forward Voltage Drop each. Of course we would want to include a current limiting resistor, right? How would you find out the voltage across that resistor? It's easy:
5 (System Voltage) = 2.4 (LED 1) + 2.4 (LED 2) + Resistor
5 = 4.8 + Resistor
Resistor = 5 - 4.8
Resistor = 0.2
So there is .2V across the resistor! This is a simplified example and it isn't always this easy, but hopefully this gives you an idea of why Forward Voltage Drop is important. Using the voltage number you derive from Kirchhoff's Laws you can also do things like determine the current across a component using Ohm's Law. In short, you want your system voltage equal to the expected forward voltage of your combined circuit components.
Calculating Current Limiting Resistors
If you need to calculate the exact current limiting resistor value in series with an LED, check out one of the example applications in the resistors tutorial for more information.
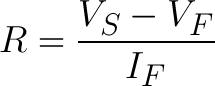 |
| Equation Used to Calculate a Current Limiting Resistor |
