Hexadecimal
Converting To/From Binary
Breathe easy! We've gotten the hard conversions out of the way. We use hex in electrical and computer engineering because it's incredibly easy to convert to and from binary -- the 1's and 0's language of computers.
Converting between hex and binary is easy, because each digit of a hexadecimal number "maps" to four bits (a bit being an individual binary digit) of a binary value. So a byte -- eight binary digits -- can always be represented by two hexadecimal digits. This makes hex a really great, concise way to represent a byte or group of bytes.
Converting from Binary to Hex
Let's begin by mapping the first 16 hexadecimal values to binary.
| Decimal | Hex | Binary | ... | Decimal | Hex | Binary |
|---|---|---|---|---|---|---|
| 00 | 0 | 0000 | 08 | 8 | 1000 | |
| 01 | 1 | 0001 | 09 | 9 | 1001 | |
| 02 | 2 | 0010 | 10 | A | 1010 | |
| 03 | 3 | 0011 | 11 | B | 1011 | |
| 04 | 4 | 0100 | 12 | C | 1100 | |
| 05 | 5 | 0101 | 13 | D | 1101 | |
| 06 | 6 | 0110 | 14 | E | 1110 | |
| 07 | 7 | 0111 | 15 | F | 1111 |
As you grow, and continue to use hex and binary, these 16 values will become ingrained in your brain. Those are the key to converting between hex and binary.
To convert between binary and hex, we want to take advantage of the fact that four binary digits (bits) map to one hex digit. Follow these steps to convert from binary to hex.
- Split a binary value into groups of four, starting at the right-most side.
- For each group of four, consult the table above to find the matching hex value, and replace groups of four binary digits with the one hex value.
That's it! Let's try it out.
Binary to Hex Example: Convert 0b101111010100001
To begin, start at the far-right of the binary number, and sort the 1's and 0's into groups of four:
| Binary Digits Sorted: | 0101 | 1110 | 1010 | 0001 |
|---|
Now consult our big table-o'-sixteen to convert the groups-of-four to a hex digit:
| Binary Digits Sorted: | 0101 | 1110 | 1010 | 0001 |
|---|---|---|---|---|
| Hex Equivalents: | 5 | E | A | 1 |
And there you have it! 0b101111010100001 = 0x5EA1. (Ugh. This tutorial has far exceeded everyone's tolerance for 1337. My apologies.)
Converting from Hex to Binary
Converting from hex to binary is a lot like converting binary to hex. Simply take a hex digit and turn it into four binary digits. Repeat until your number is full of 0's and 1's.
Hex to Binary Example: Convert 0xDEADBEEF
To convert 0xDEADBEEF (a commonly used code to indicate a system crash), begin by sorting the digits into "bins":
| Hex Digits Sorted: | D | E | A | D | B | E | E | F |
|---|
Then convert each hex digit into four bits:
| Hex Digits Sorted: | D | E | A | D | B | E | E | F |
|---|---|---|---|---|---|---|---|---|
| Hex Digits Sorted: | 1101 | 1110 | 1010 | 1101 | 1011 | 1110 | 1110 | 1111 |
In other words, 0xDEADBEEF = 0b11011110101011011011111011101111. That's a lot of 1's and 0's.
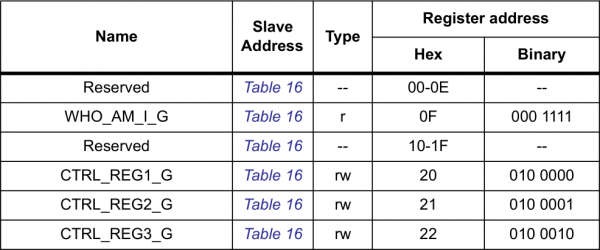
Use Hex to Represent and Identify Bytes
The examples above show off one of hex's greatest powers: easily representing values of bytes. Hex is often easier for us to work with because the values are shorter and more memorable than a long string of 1's and 0's.
For example, the register map above is from the LSM9DS0 (a nifty, 9DOF sensor). It lists register addresses, which are used to control the sensor, in both hex and binary. If you want to access the CTRL_REG2_G register, it's much easier to remember 0x21 than 0b010001, and discovering a typo in the hex value is much easier than in binary. For that reason, we're much more likely to use hex values in our code than their binary equivalents.