GeoFence Treasure Hunt With Artemis Global Tracker

The Logic

The code enables the GNSS module funcitonality, finds the current longitude and latitude of the AGT device, randomly generates a target distance and angle based on the current location, and begins blinking the onboard LED with intervals relating to the distance between the current location and target location. We will also mark the location of a 30 meter radius around the starting location using the “addGeofence” function from the SparkFun u-blox GNSS Arduino Library. If the device leaves this radius while playing the game, the player will lose. The treasure position is chosen by randomly selecting a distance between 15 and 30 meters and a distance between 0 and 360 degrees from the starting position.

The magic here involves calculating distances and angles with spherical coordinates. The game should be playable on a large (potentially worldly) scale, which means no assuming the Earth is flat. Therefore, from two sets of spherical coordinates (the initial and current position of the AGT device), we need to compute the effective spherical angle and distance between them. Through research, making use of the haversine and bearing equations, where the haversine function calculates the distance between the two positions and the bearing function calculates the angle, seemed like the best approach. They work as follows:

Haversine Distance Function

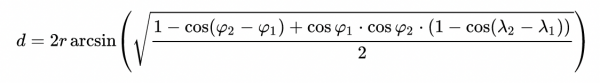
// GET COORDINATE DISTANCE - HAVERSINE FORMULA

double getCoordinateDistance(long La1, long Lo1, double La2, long Lo2) {
    double radius = 6.3781e6;  // radius of the Earth (meters)
    // conversion to radians
    double rla1 = La1*(1E-7) * (PI/180);
    double rla2 = La2*(1E-7) * (PI/180);
    double rlo1 = Lo1*(1E-7) * (PI/180);
    double rlo2 = Lo2*(1E-7) * (PI/180);

    double a = sin((rla2-rla1)/2) * sin((rla2-rla1)/2) + cos(rla1) * cos(rla2) * sin((rlo2 - rlo1)/2) * sin((rlo2 - rlo1)/2);

    double b = 2 * atan2(sqrt(a), sqrt(1-a));

    return radius * b;

Bearing Angle Function

// GET COORDINATE ANGLE (BEARING) HELPER
long getCoordinateBearing(long La1, long Lo1, long La2, long Lo2) {
    double rLa1 = La1*(1E-7) * (PI/180);
    double rLa2 = La2*(1E-7) * (PI/180);
    double rLo1 = Lo1*(1E-7) * (PI/180);
    double rLo2 = Lo2*(1E-7) * (PI/180);

    double y = sin(rLo2-rLo1) * cos(rLa2);
    double x = cos(rLa1) * sin(rLa2) - sin(rLa1)*cos(rLa2)*cos(rLo2-rLo1);

    return (atan2(y, x) * (180/PI)); // returns angle between -180 and 180

The necessity of these functions becomes apparent once you learn about the system of spherical coordinates. Longitudinal values may work as expected, associated with a vertical position on a sphere. However, Latitudinal distances become difficult to calculate since each longitudinal value forces each horizontal cross-section of the Earth to be a different sized circle.

With these functions, we calculate the current positions angle and distance from the initial position, essentially creating polar coordinates. Once the distance between the target and current polar coordinates reaches a certain threshold (within 2 meters), the treasure has been found! The distance to the target is also made aware to the player visually through an LED meter as shown in the demo. In order to find this distance we use the polar distance formula as shown:

As the player gets closer to the goal position, the onboard LED blinks faster and faster until it stays lit when the treasure is found. Also, the AGT is writing to the Arduino Serial Monitor with the current player positions, the goal positions, and a message demonstrating how close the player is to the treasure (“hotter”, “colder, etc)