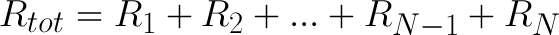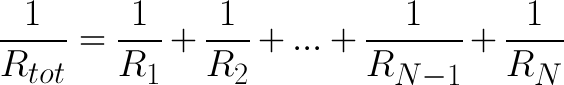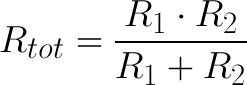Resistors
Series and Parallel Resistors
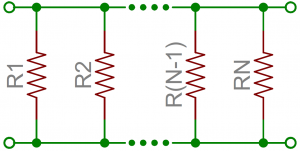
Resistors are paired together all the time in electronics, usually in either a series or parallel circuit. When resistors are combined in series or parallel, they create a total resistance, which can be calculated using one of two equations. Knowing how resistor values combine comes in handy if you need to create a specific resistor value.
Series resistors
When connected in series resistor values simply add up.
So, for example, if you just have to have a 12.33kΩ resistor, seek out some of the more common resistor values of 12kΩ and 330Ω, and butt them up together in series.
Parallel resistors
Finding the resistance of resistors in parallel isn't quite so easy. The total resistance of N resistors in parallel is the inverse of the sum of all inverse resistances. This equation might make more sense than that last sentence:
(The inverse of resistance is actually called conductance, so put more succinctly: the conductance of parallel resistors is the sum of each of their conductances).
As a special case of this equation: if you have just two resistors in parallel, their total resistance can be calculated with this slightly-less-inverted equation:
As an even more special case of that equation, if you have two parallel resistors of equal value the total resistance is half of their value. For example, if two 10kΩ resistors are in parallel, their total resistance is 5kΩ.
A shorthand way of saying two resistors are in parallel is by using the parallel operator: ||. For example, if R1 is in parallel with R2, the conceptual equation could be written as R1||R2. Much cleaner, and hides all those nasty fractions!
Resistor networks
As a special introduction to calculating total resistances, electronics teachers just love to subject their students to finding that of crazy, convoluted resistor networks.
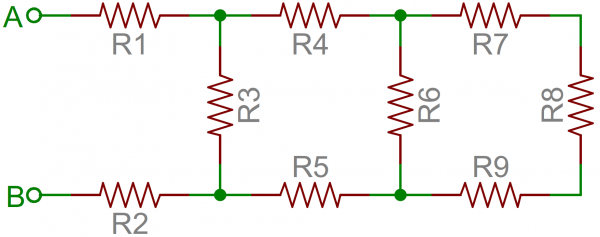
A tame resistor network question might be something like: "what's the resistance from terminals A to B in this circuit?"
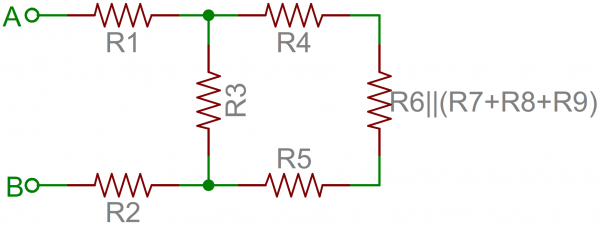
To solve such a problem, start at the back-end of the circuit and simplify towards the two terminals. In this case R7, R8 and R9 are all in series and can be added together. Those three resistors are in parallel with R6, so those four resistors could be turned into one with a resistance of R6||(R7+R8+R9). Making our circuit:
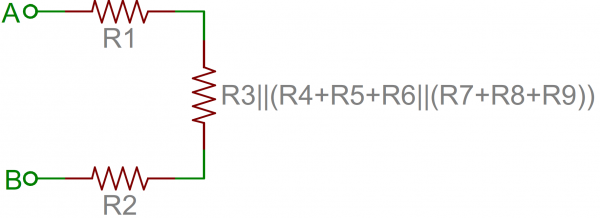
Now the four right-most resistors can be simplified even further. R4, R5 and our conglomeration of R6 - R9 are all in series and can be added. Then those series resistors are all in parallel with R3.
And that's just three series resistors between the A and B terminals. Add 'em on up! So the total resistance of that circuit is: R1+R2+R3||(R4+R5+R6||(R7+R8+R9)).