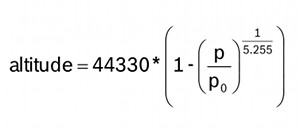BMP180 Barometric Pressure Sensor Hookup

Contributors: MikeGrusin

Measuring Weather and Altitude

The BMP180 was designed to accurately measure atmospheric pressure. Atmospheric pressure varies with both weather and altitude; you can measure both of these using this sensor. Here's how:

What is Atmospheric Pressure?

The definition of pressure is a force "pressing" on an area. A common unit of pressure is pounds per square inch (psi). One pound, pressing on one square inch, equals one psi. The SI unit is newtons per square meter, which are called pascals (Pa).

There are lots of situations in which pressure can be measured (gravity, pull, etc.), but right now we're interested in atmospheric pressure, which is the force that the air around you is exerting on everything. The weight of the gasses in the atmosphere creates atmospheric pressure. One doesn't normally notice that air weighs anything, but if you took a one inch wide column of air from sea level to the top of the atmosphere, it would weigh about 14.7 pounds. (A 1 cm wide column of air would weigh about 1 kg.) This weight, pressing down on the footprint of that column, creates the atmospheric pressure that we can measure with sensors like the BMP180.

Because that inch-wide column of air weighs about 14.7 pounds, and is pressing on one square inch, it follows that the average sea level pressure is about 14.7 pounds per square inch (psi), or 101325 pascals. This will drop about 4% for each 1000 feet (or 300 meters) you ascend. The higher you get, the less pressure you'll see, because the column to the top of the atmosphere is that much shorter and therefore weighs less. This is useful to know, because by measuring the pressure and doing some math, you can determine your altitude.

Fun fact: The air pressure at 12,500 feet (3810 meters) is only half of that at sea level. In other words, half of the mass of the atmosphere is below 12,500 feet, and the air at 12,500 feet is half as dense as that at sea level. No wonder you have a harder time breathing up there.

The BMP180 outputs absolute pressure in pascals (Pa). One pascal is a very small amount of pressure, approximately the amount that a sheet of paper will exert resting on a table. You will more often see measurements in hectopascals (1 hPa = 100 Pa) or kilopascals (1 kPa = 1000 Pa). The Arduino library we've provided outputs floating-point values in hPa, which also happens to equal one millibar (mbar).

Here are some conversions to other pressure units:

1 hPa = 100 Pa = 1 mbar = 0.001 bar

1 hPa = 0.75006168 Torr

1 hPa = 0.01450377 psi (pounds per square inch)

1 hPa = 0.02953337 inHg (inches of mercury)

1 hpa = 0.00098692 atm (standard atmospheres)

Temperature Effects

Because temperature affects the density of a gas, and density affects the mass of a gas, and mass affects the pressure (whew), atmospheric pressure will change dramatically with temperature. Pilots know this as "density altitude", which makes it easier to take off on a cold day than a hot one because the air is more dense and has a greater aerodynamic effect.

To compensate for temperature, the BMP180 includes a rather good temperature sensor as well as a pressure sensor. To perform a pressure reading, you first take a temperature reading, then combine that with a raw pressure reading to come up with a final temperature-compensated pressure measurement. (Don't worry, the Arduino library makes all of this very easy.)

Measuring Absolute Pressure

As we just mentioned, if your application requires measuring absolute pressure, all you have to do is get a temperature reading, then perform a pressure reading (see the example sketch for details). The final pressure reading will be in hPa = mbar. If you wish, you can convert this to a different unit using the above conversion factors.

Note that the absolute pressure of the atmosphere will vary with both your altitude and the current weather patterns, both of which are useful things to measure.

Weather Observations

The atmospheric pressure at any given location on earth (or anywhere with an atmosphere) isn't constant. The complex interaction between the earth's spin, axis tilt, and many other factors result in moving areas of higher and lower pressure, which in turn cause the variations in weather we see every day. By watching for changes in pressure, you can predict short-term changes in the weather. For example, dropping pressure usually means wet weather or a storm is approaching (a low-pressure system is moving in). Rising pressure usually means that clear weather is approaching (a high-pressure system is moving through).

But remember that atmospheric pressure also varies with altitude. The absolute pressure in Denver (altitude 5280') will always be lower than the absolute pressure in San Francisco (altitude 52'). If weather stations just reported their absolute pressure, it would be difficult to directly compare pressure measurements from one location to another (and large-scale weather predictions depend on measurements from as many stations as possible).

To solve this problem, weather stations always remove the effects of altitude from their reported pressure readings by mathematically adding the equivalent fixed pressure to make it appear as if the reading was taken at sea level. When you do this, a higher reading in San Francisco than Denver will always be because of weather patterns, and not because of altitude.

To do this, there is a function in the library called seaLevel(P,A). This takes absolute pressure (P) in hPa, and the station's current altitude (A) in meters, and removes the effects of the altitude from the pressure. You can use the output of this function to directly compare your weather readings to other stations around the world.

For more information, here is a good Wikipedia article on mean sea level pressure.

Determining Altitude

Since pressure varies with altitude, you can use a pressure sensor to measure altitude (with a few caveats).

The average pressure of the atmosphere at sea level is 1013.25 hPa (or mbar). This drops off to zero as you climb towards the vacuum of space. Because the curve of this drop-off is well understood, you can compute the altitude difference between two pressure measurements (p and p₀) by using this equation:

There are two ways you can take advantage of this.

1. If you use sea level pressure (1013.25 hPa) as the baseline pressure (p₀), the output of the equation will be your current altitude above sea level.

2. Or, if you take a single pressure reading at your current location, and use that as your baseline (p₀), all subsequent pressure readings will result in relative altitude changes from the baseline. Climb the stairs and you should see the altitude go from zero to 3 or 4 meters. Go down to the basement, and you'll see -3 or -4 meters. There's an example sketch included with the library called BMP180_altitude_example.ino that shows how to do this.

There's a function in the library called altitude(P,P0) that lets you accomplish both of these things. If you give it the sea level pressure (1013.25 hPa) for p₀, and your local pressure for p, it will give you your altitude above sea level. If you use a local pressure measurement for p₀, subsequent p pressure readings will give you your change in altitude from the baseline.

Now for the caveats:

Accuracy: How accurate is this? The theoretical noise level at the BMP180s highest resolution is 0.25m (about 10 inches), though in practice we see noise on the order of 1m (40 inches). You can improve the accuracy by taking a large number of readings and averaging them, although this will slow down your sample rate and response time.

Weather: You should also remember that pressure changes due to weather will affect your altitude readings. The best accuracy will be obtained if you take a "fresh" p₀ when you need it and don't rely on it to be accurate for extended periods due to changes in the weather.

Maximum altitude: The BMP180 can't measure all the way down to vacuum (or up to space). It's advertised lower limit is about 300 hPa (or mbar), which corresponds to an altitude of about 3000m or 30,000 feet. People have flown these to higher altitudes and gotten useful results, but this isn't guaranteed or likely to be accurate. (You might consider using GPS for high-altitude measurements).

Minimum altitude: Similarly, this sensor isn't suited for large pressures either. The advertised upper limit is 1100 hPa=mbar (or 16 psi), which is about 500 feet below sea level (that's in air - the BMP180 isn't submersible in water). This sensor isn't a good choice for submersible or compressed-gas measurements.