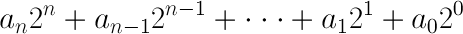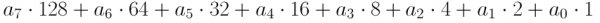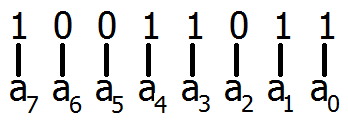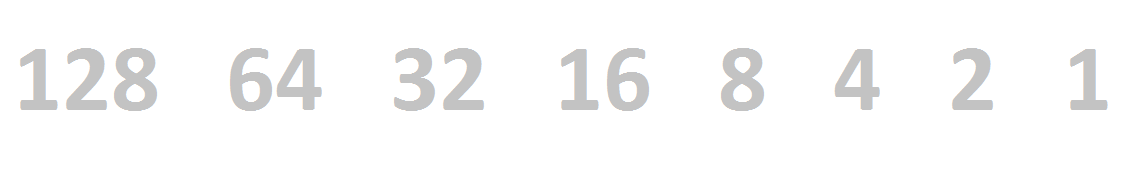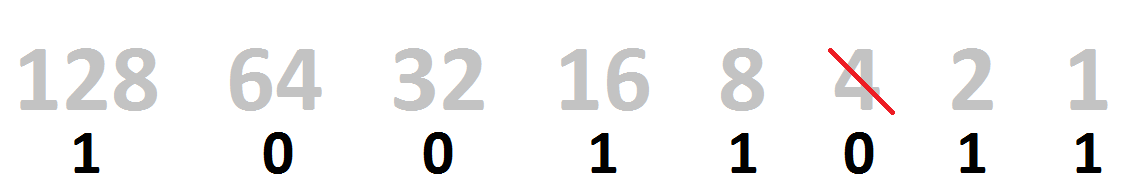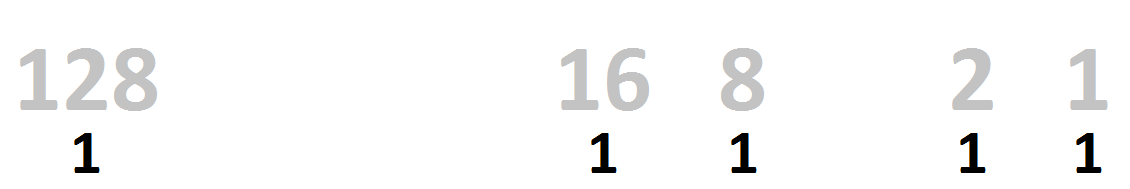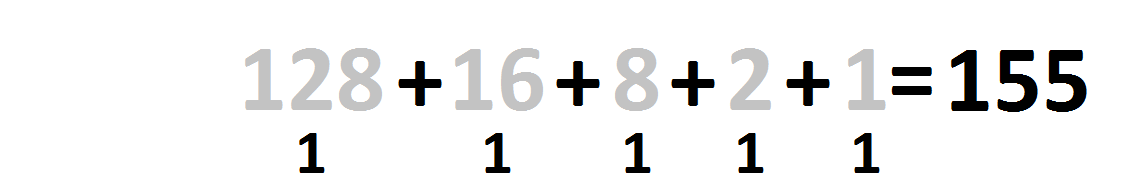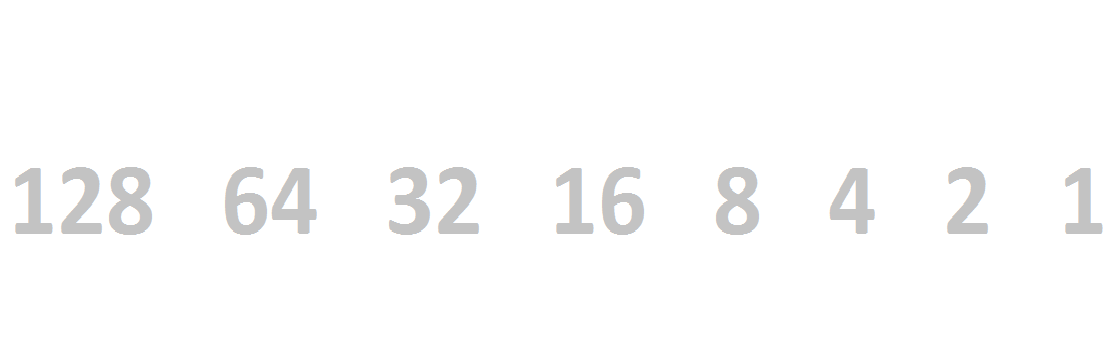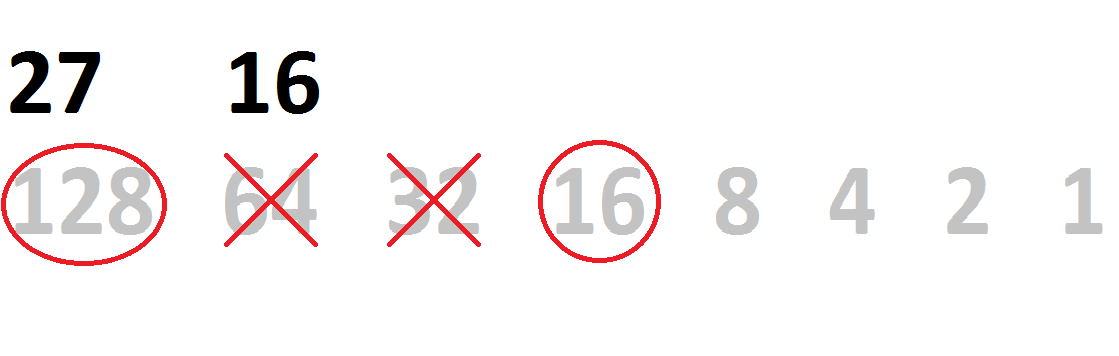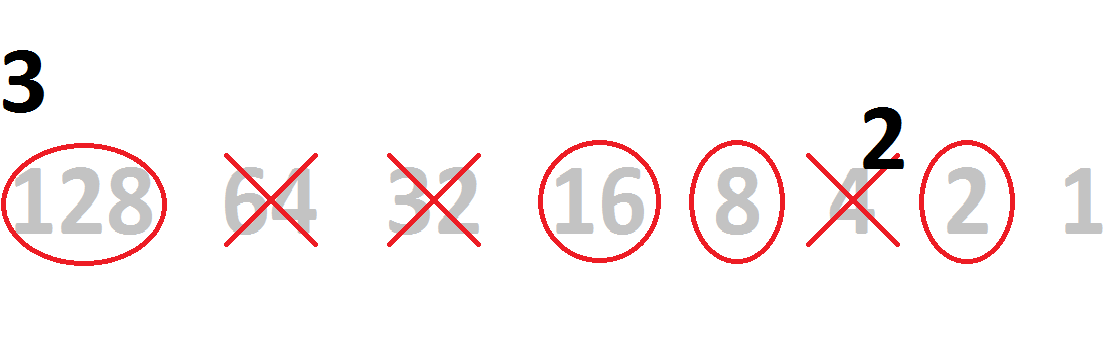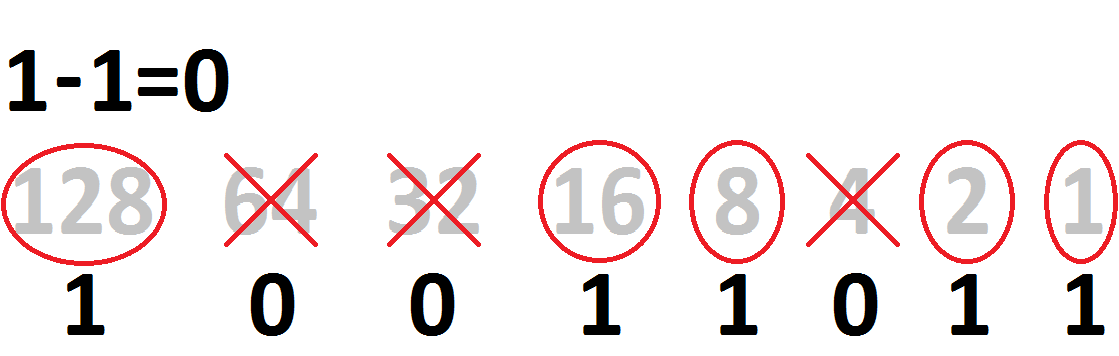Binary
ABC's of 1's and 0's
Prepare to have your perception of reality shattered. Everything you ever thought you knew about something so simple as numbers is going to change. All your life you thought having 100 somethings meant having this many:
When, really, it only meant having this many:
No, Rod Serling’s not about to cross into the frame, and you haven’t swallowed any red pills. You’ve entered the binary zone and have just encountered base numbering systems.
Number Systems and Bases
Number systems are the methods we use to represent numbers. Since grade school, we’ve all been mostly operating within the comfy confines of a base-10 number system, but there are many others. Base-2, base-8, base-16, base-20, base...you get the point. There are an infinite variety of base-number systems out there, but only a few are especially important to electrical engineering.
The really popular number systems even have their own name. Base-10, for example, is commonly referred to as the decimal number system. Base-2, which we’re here to talk about today, also goes by the moniker of binary. Another popular numeral system, base-16, is called hexadecimal.
The base of a number is often represented by a subscripted integer trailing a value. So in the introduction above, the first image would actually be 10010 somethings while the second image would be 1002 somethings. This is a handy way to specify a number’s base when there’s ever any possibility of ambiguity.
Why Binary?
Why binary you ask? Well, why decimal? We’ve been using decimal forever and have mostly taken for granted the reason we settled on the base-10 number system for our everyday number needs. Maybe it’s because we have 10 fingers, or maybe it’s just because the Romans forced it upon their ancient subjugates. Regardless of what lead to it, tricks we’ve learned along the way have solidified base-10’s place in our heart; everyone can count by 10’s. We even round large numbers to the nearest multiple of 10. We’re obsessed with 10!
Computers and electronics are rather limited in the finger-and-toe department. At the lowest level, they really only have two ways to represent the state of anything: ON or OFF, high or low, 1 or 0. And so, almost all electronics rely on a base-2 number system to store, manipulate, and math numbers.
The heavy reliance electronics place on binary numbers means it’s important to know how the base-2 number system works. You’ll commonly encounter binary, or its cousins, like hexadecimal, all over computer programs. Analysis of Digital logic circuits and other very low-level electronics also requires heavy use of binary.
In this tutorial, you’ll find that anything you can do to a decimal number can also be done to a binary number. Some operations may be even easier to do on a binary number (though others can be more painful). We’ll cover all of that and more in this tutorial.
Suggested Reading
We’re reaching pretty deep into the concepts bin. A lot of this tutorial builds on mathematical concepts like addition, multiplication, division (including remainders), and exponents.
No previous knowledge of electronics is required (except for knowing how the base-10 system works, which most people do), but we do observe how binary is used in Arduino programming, and knowing something about data types could come in handy. In addition, knowledge of digital logic will help to supplement all of this binary business.
Counting and Converting
The base of each number system is also called the radix. The radix of a decimal number is ten, and the radix of binary is two. The radix determines how many different symbols are required in order to flesh out a number system. In our decimal number system we’ve got 10 numeral representations for values between nothing and ten somethings: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Each of those symbols represents a very specific, standardized value.
In binary we’re only allowed two symbols: 0 and 1. But using those two symbols we can create any number that a decimal system can.
Counting in binary
You can count in decimal endlessly, even in your sleep, but how would you count in binary? Zero and one in base-two should look pretty familiar: 0 and 1. From there things get decidedly binary.
Remember that we’ve only got those two digits, so as we do in decimal, when we run out of symbols we’ve got to shift one column to the left, add a 1, and turn all of the digits to right to 0. So after 1 we get 10, then 11, then 100. Let’s start counting...
| Decimal | Binary | ... | Decimal | Binary |
| 0 | 0 | 16 | 10000 | |
| 1 | 1 | 17 | 10001 | |
| 2 | 10 | 18 | 10010 | |
| 3 | 11 | 19 | 10011 | |
| 4 | 100 | 20 | 10100 | |
| 5 | 101 | 21 | 10101 | |
| 6 | 110 | 22 | 10110 | |
| 7 | 111 | 23 | 10111 | |
| 8 | 1000 | 24 | 11000 | |
| 9 | 1001 | 25 | 11001 | |
| 10 | 1010 | 26 | 11010 | |
| 11 | 1011 | 27 | 11011 | |
| 12 | 1100 | 28 | 11100 | |
| 13 | 1101 | 29 | 11101 | |
| 14 | 1110 | 30 | 11110 | |
| 15 | 1111 | 31 | 11111 |
Does that start to paint the picture? Let’s examine how we might convert from those binary numbers to decimal.
Converting binary to decimal
There's no one way to convert binary-to-decimal. We'll outline two methods below, the more "mathy" method, and another that's more visual. We'll cover both, but if the first uses too much ugly terminology skip down to the second.
Method 1
There's a handy function we can use to convert any binary number to decimal:
There are four important elements to that equation:
- an, an-1, a1, etc., are the digits of a number. These are the 0's and 1's you're familiar with, but in binary they can only be 0 or 1.
- The position of a digit is also important to observe. The position starts at 0, on the right-most digit; this 1 or 0 is the least-significant. Every digit you move to the left increases in significance, and also increases the position by 1.
- The length of a binary number is given by the value of n, actually it's n+1. For example, a binary number like 101 has a length of 3, something larger, like 10011110 has a length of 8.
- Each digit is multiplied by a weight: the 2n, 2n-1, 21, etc. The right-most weight - 20 equates to 1, move one digit to the left and the weight becomes 2, then 4, 8, 16, 32, 64, 128, 256,... and on and on. Powers of two are of great importance to binary, they quickly become very familiar.
Let's get rid of those n's and exponents, and carry out our binary positional notation equation out eight positions:
Taking that further, let's plug in some values for the digits. What if you had a binary number like: 10011011? That would mean an values of:
For the sake of this tutorial, assume that the right-most value is always the least-significant. The least-significant digit in a number is the digit that has the smallest influence on a number’s ultimate value. The significance of the digits is arbitrary - part of a convention called endianness. A binary number can be either big-endian, where the most-significant digit is the left-most, or little-endian which we’ll use in this tutorial (and you’ll usually see binary numbers written this way).
Now, plug those digits into our binary to decimal equation. Because our number is little-endian the least-significant value should be multiplied by the smallest weight.
1 * 27 + 0 * 26 + 0 * 25 + 1 * 24 + 1 * 23 + 0 * 22 + 1 * 21 + 1 * 20And we can simplify it down to find our decimal number:
= 1 * 128 + 0 * 64 + 0 * 32 + 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1
= 128 + 16 + 8 + 2 + 1
= 155
You’ll quickly notice that it takes many more digits to represent a number in binary than it does in decimal, but it’s all done with just two digits!
Method 2
Another, more visual way to convert binary numbers to decimal is to begin by sorting each 1 and 0 into a bin. Each bin has a successive power of two weight to it, the 1, 2, 4, 8, 16,... we’re used to. Carrying it out eight places would look something like this:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
So, if we sorted our 10011011 binary number into those bins, it’d look like this:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
For every bin that has a binary 0 value in it, just cross out and remove it.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
And then add up any remaining weights to get your number!
Converting from decimal to binary
Just like going from binary to decimal, there's more than one way to convert decimal to binary. The first uses division and remainders, and the second uses subtraction. Try both, or stick to one you're comfortable with!
Method 1
It isn’t quite as simple to convert a decimal number to binary. This conversion requires repeatedly dividing the decimal number by 2, until you’ve reduced it to zero. Every time you divide the remainder of the division becomes a digit in the binary number you’re creating.
Don't remember how to do remainders? If it's been a while, remember that, since we're dividing by two, if the dividend is even, the remainder will be 0; an odd dividend means a remainder of 1.
For example, to convert 155 to binary you’d go through this process:
155 ÷ 2 = 77 R 1 (That’s the right-most digit, 1st position)
77 ÷ 2 = 38 R 1 (2nd position)
38 ÷ 2 = 19 R 0 (3rd position)
19 ÷ 2 = 9 R 1
9 ÷ 2 = 4 R 1
4 ÷ 2 = 2 R 0
2 ÷ 2 = 1 R 0
1 ÷ 2 = 0 R 1 (8th position)
The first remainder is the least-significant (right-most) digit, so read from top-to-bottom to flesh out our binary number right-to-left: 10011011. Match it up to the example above...that’s a bingo!
Method 2
If dividing and finding remainders isn’t your thing, there may be an easier method for converting decimal to binary. Start by finding the largest power of two that’s still smaller than your decimal number, and subtract it from the decimal. Then, continue to subtract by the largest possible power of two until you get to zero. Every weight-position that was subtracted, gets a binary 1 digit; digits that weren’t subtracted get a 0.
Continuing with our example, 155 can be subtracted by 128, producing 27:
| 155 - 128 = 27 | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | |||||||
Our new number, 27, can’t be subtracted by either 64 or 32. Both of those positions get a 0. We can subtract by 16, producing 11.
| 27 - 16 = 11 | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | ||||
And 8 subtracts from 11, producing 3. After that, no such luck with 4.
| 11 - 8 = 3 | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | ||
Our 3 can be subtracted by 2, producing 1. And finally, the 1 subtracts by 1 to make 0.
| 3 - 2 = 1 | |||||||
| 1 - 1 = 0 | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
We’ve got a binary number!
Conversion calculators
Fortunately, there are tons of binary-to-decimal and vice-versa calculators out there. You shouldn’t often need to resort to long-hand conversion.
Here! Plug some numbers into these boxes, and the other should magically change.
Make sure you only put 1's or 0's in the binary box, and 0-9 in the decimal one. Have fun!
Bits, Nibbles, and Bytes
In discussing the make of a binary number, we briefly covered the length of the number. The length of a binary number is the amount of 1's and 0's it has.
Common binary number lengths
Binary values are often grouped into a common length of 1’s and 0’s, this number of digits is called the length of a number. Common bit-lengths of binary numbers include bits, nibbles, and bytes (hungry yet?). Each 1 or 0 in a binary number is called a bit. From there, a group of 4 bits is called a nibble, and 8-bits makes a byte.
Bytes are a pretty common buzzword when working in binary. Processors are all built to work with a set length of bits, which is usually this length is a multiple of a byte: 8, 16, 32, 64, etc.
To sum it up:
| Length | Name | Example |
| 1 | Bit | 0 |
| 4 | Nibble | 1011 |
| 8 | Byte | 10110101 |
Word is another length buzzword that gets thrown out from time-to-time. Word is much less yummy sounding and much more ambiguous. The length of a word is usually dependent on the architecture of a processor. It could be 16-bits, 32, 64, or even more.
Padding with leading zeros
You might see binary values represented in bytes (or more), even if making a number 8-bits-long requires adding leading zeros. Leading zeros are one or more 0’s added to the left of the most-significant 1-bit in a number. You usually don't see leading zeros in a decimal number: 007 doesn't tell you any more about the value of a number 7 (it might say something else).
Leading zeros aren't required on binary values, but they do help present information about the bit-length of a number. For example, you may see the number 1 printed as 00000001, just to tell you we're working within the realm of a byte. Both numbers represent the same value, however, the number with seven 0’s in front adds information about the bit-length of a value.
Bitwise Operators
There are a number of ways to manipulate binary values. Just as you can with decimal numbers, you can perform standard mathematical operations - addition, subtraction, multiplication, division - on binary values (which we’ll cover on the next page). You can also manipulate individual bits of a binary value using bitwise operators.
Bitwise operators perform functions bit-by-bit on either one or two full binary numbers. They make use of boolean logic operating on a group of binary symbols. These bitwise operators are widely used throughout both electronics and programming.
Complement (NOT)
The complement of a binary value is like finding the exact opposite of everything about it. The complement function looks at a number and turns every 1 into a 0 and every 0 becomes a 1. The complement operator is also called NOT.
For example to find the complement of 10110101:
NOT 10110101 (decimal 181)
-------- =
01001010 (decimal 74)
NOT is the only bitwise operator which only operates on a single binary value.
OR
OR takes two numbers and produces the union of them. Here’s the process to OR two binary numbers together: line up each number so the bits match up, then compare each of their bits that share a position. For each bit comparison, if either or both bits are 1, the value of the result at that bit-position is 1. If both values have a 0 at that position, the result also gets a 0 at that position.
The four possible OR combinations, and their outcome are:
- 0 OR 0 = 0
- 0 OR 1 = 1
- 1 OR 0 = 1
- 1 OR 1 = 1
For example to find the 10011010 OR 01000110, line up each of the numbers bit-by-bit. If either or both numbers has a 1 in a column, the result value has a 1 there too:
10011010
OR 01000110
-------- =
11011110
Think of the OR operation as binary addition, without a carry-over. 0 plus 0 is 0, but 1 plus anything will be 1.
AND
AND takes two numbers and produces the conjunction of them. AND will only produce a 1 if both of the values it’s operating on are also 1.
The process of AND'ing two binary values together is similar to that of OR. Line up each number so the bits match up, then compare each of their bits that share a position. For each bit comparison, if either or both bits are 0, the value of the result at that bit-position is 0. If both values have a 1 at that position, the result also gets a 1 at that position.
The four possible AND combinations, and their outcome are:
- 0 AND 0 = 0
- 0 AND 1 = 0
- 1 AND 0 = 0
- 1 AND 1 = 1
For example, to find the value of 10011010 AND 01000110, start by lining up each value. The result of each bit-position will only be 1 if both bits in that column are also 1.
10011010
AND 01000110
-------- =
00000010
Think of AND as kind of like multiplication. Whenever you multiply by 0 the result will also be 0.
XOR
XOR is the exclusive OR. XOR behaves like regular OR, except it’ll only produce a 1 if either one or the other numbers has a 1 in that bit-position.
The four possible XOR combinations, and their outcome are:
- 0 XOR 0 = 0
- 0 XOR 1 = 1
- 1 XOR 0 = 1
- 1 XOR 1 = 0
For example, to find the result of 10011010 XOR 01000110:
10011010
XOR 01000110
-------- =
11011100
Notice the 2nd bit, a 0 resulting from two 1’s XOR’ed together.
Bit shifts
Bit shifts aren’t necessarily a bitwise operator like those listed above, but they are a handy tool in manipulating a single binary value.
There are two components to a bit shift - the direction and the amount of bits to shift. You can shift a number either to the left or right, and you can shift by one bit or many bits.
When shifting to the right, one or more of the least-significant bits (on the right-side of the number) just get cut off, shifted into the infinite nothing. Leading zeros can be added to keep the bit-length the same.
For example, shifting 10011010 to the right two bits:
RIGHT-SHIFT-2 10011010 (decimal 154)
-------- =
00100110 (decimal 38)
Shifting to the left adds pushes all of the bits toward the most-significant side (the left-side) of the number. For each shift, a zero is added in the least-significant-bit position.
For example, shifting 10011010 to the left one bit:
LEFT-SHIFT-1 10011010 (decimal 154)
-------- =
100110100 (decimal 308)
That simple bit shift actually performs a relatively complicated mathematical function. Shifts to the left n bits multiplies a number by 2n (see how the last example multiplied the input by two?), while a shift n bits to the right will do an integer divide by 2n. Shifting to the right to divide can get weird - any fractions produced by the shift division will be chopped off, which is why 154 shifted right twice equals 38 instead of 154/4=38.5. Bit shifts can be a powerfully fast way to divide or multiply by 2, 4, 8, etc.
These bitwise operators provide us most of the tools necessary to do standard mathematical operations on binary numbers.
Binary in Programming
At their very lowest-level, binary is what drives all electronics. As such, encountering binary in computer programming is inevitable.
Representing binary values in a program
In Arduino, and most other programming languages, a binary number can be represented by a 0b preceding the binary number. Without that 0b the number will just be a decimal number.
For example, these two numbers in code would produce two very different values:
a = 0b01101010; // Decimal 106
c = 01101010; // Decimal 1,101,010 - no 0b prefix means decimal
Bitwise operators in programming
Each of the bitwise operators discussed a few pages ago can be performed in a programming language.
AND bitwise operator
To AND two different binary values, use the ampersand, &, operator. For example:
x = 0b10011010 & 0b01000110;
// x would equal 0b00000010
AND’ing a binary value is useful if you need to apply a bit-mask to a value, or check if a specific bit in a binary number is 1.
The AND bitwise operator shouldn’t be confused with the AND conditional operation, which uses the double-ampersand (&&) and produces a true or false based on the input of multiple logic statements.
OR bitwise operator
The OR bitwise operator is the pipe | (shift+\, the key below backspace). For example:
y = 0b10011010 | 0b01000110;
// y would equal 0b11011110
OR’ing a binary value is useful if you want to set one or more bits in a number to be 1.
As with AND, make sure you don’t switch up the OR bitwise operator with the OR conditional operator - the double-pipe (||).
NOT bitwise operator
The bitwise NOT operator is the tilde ~ (shift+`, the key above tab). As an example:
z = ~(0b10100110);
// z would equal 0b01011001
XOR bitwise operator
To XOR two values use the caret (^) between them:
r = 0b10011010 ^ 0b01000110;
// r would equal 0b11011100
XOR is useful for checking if bits are different, because it'll only result in a 1 if it operates on both a 0 or 1.
Shifting left and right
To shift a binary number left or right n bits, use the <<n or >>n operators. A couple examples:
i = 0b10100101 << 4; // Shift i left 4 bits
// i would equal 0b101001010000
j = 0b10010010 >> 2; // Shift j right 2 bits
// j would equal 0b00100100
Shift's are an especially efficient way to multiply or divide by powers of two. In the example above, shifting four units to the left multiplies that value by 24 (16). The second example, shifting two bits to the right, would divide that number by 22 (4).
Interested in learning more foundational topics?
See our Engineering Essentials page for a full list of cornerstone topics surrounding electrical engineering.
Resources and Going Further
Binary is the building block of all computations, calculations, and operations in electronics. So there are many places to go from here.
Are you interested in learning more about binary, and other important numeral systems?
- Binary Blaster Hookup Guide -- If you're looking to practice your binary conversions, the Binary Blaster Kit can be a great help. This is a soldering kit. Once you've put it together, use it to test your knowledge of how binary, hex, and decimal are related.
- Hexadecimal - Learn about this base-16 numeral system and how it relates to binary and decimal.
Now that you can convert between decimal and binary, you can apply that knowledge to understanding how characters are encoded universally:
Or you can apply your shiny new knowledge to low-level circuits and IC's:
You can also have a look at how binary plays an important role in this communication protocols: