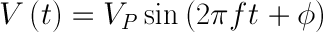Alternating Current (AC) vs. Direct Current (DC)
Alternating Current (AC)
Alternating current describes the flow of charge that changes direction periodically. As a result, the voltage level also reverses along with the current. AC is used to deliver power to houses, office buildings, etc.
Generating AC
AC can be produced using a device called an alternator. This device is a special type of electrical generator designed to produce alternating current.
A loop of wire is spun inside of a magnetic field, which induces a current along the wire. The rotation of the wire can come from any number of means: a wind turbine, a steam turbine, flowing water, and so on. Because the wire spins and enters a different magnetic polarity periodically, the voltage and current alternates on the wire. Here is a short animation showing this principle:
Generating AC can be compared to our previous water analogy:
To generate AC in a set of water pipes, we connect a mechanical crank to a piston that moves water in the pipes back and forth (our "alternating" current). Notice that the pinched section of pipe still provides resistance to the flow of water regardless of the direction of flow.
Waveforms
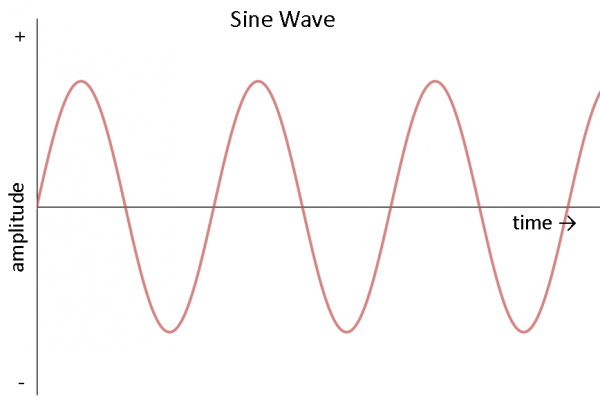
AC can come in a number of forms, as long as the voltage and current are alternating. If we hook up an oscilloscope to a circuit with AC and plot its voltage over time, we might see a number of different waveforms. The most common type of AC is the sine wave. The AC in most homes and offices have an oscillating voltage that produces a sine wave.
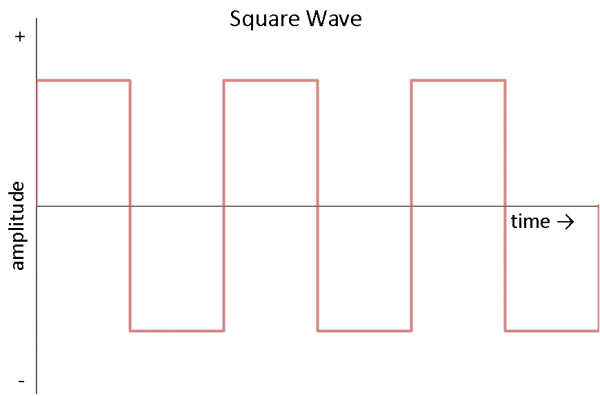
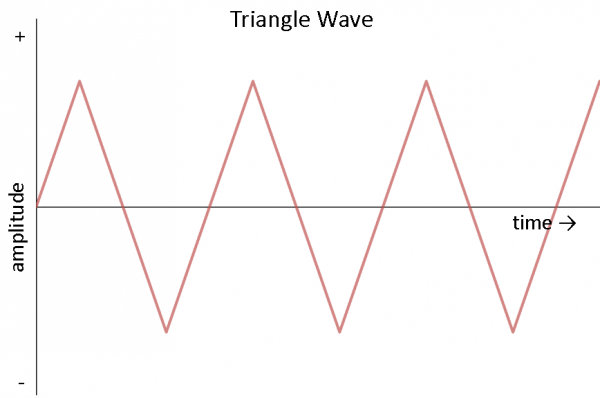
Other common forms of AC include the square wave and the triangle wave:
Square waves are often used in digital and switching electronics to test their operation.
Triangle waves are found in sound synthesis and are useful for testing linear electronics like amplifiers.

Expecting a Pay Wall?
Not Our Style.
Describing a Sine Wave
We often want to describe an AC waveform in mathematical terms. For this example, we will use the common sine wave. There are three parts to a sine wave: amplitude, frequency, and phase.
Looking at just voltage, we can describe a sine wave as the mathematical function:
V(t) is our voltage as a function of time, which means that our voltage changes as time changes. The equation to the right of the equals sign describes how the voltage changes over time.
VP is the amplitude. This describes the maximum voltage that our sine wave can reach in either direction, meaning that our voltage can be +VP volts, -VP volts, or somewhere in between.
The sin() function indicates that our voltage will be in the form of a periodic sine wave, which is a smooth oscillation around 0V.
2π is a constant that converts the freqency from cycles (in hertz) to angular frequnecy (radians per second).
f describes the frequency of the sine wave. This is given in the form of hertz or units per second. The frequency tells how many times a particular wave form (in this case, one cycle of our sine wave - a rise and a fall) occurs within one second.
t is our independent variable: time (measured in seconds). As time varies, our waveform varies.
φ describes the phase of the sine wave. Phase is a measure of how shifted the waveform is with respect to time. It is often given as a number between 0 and 360 and measured in degrees. Because of the periodic nature of the sine wave, if the wave form is shifted by 360° it becomes the same waveform again, as if it was shifted by 0°. For simplicity, we sill assume that phase is 0° for the rest of this tutorial.
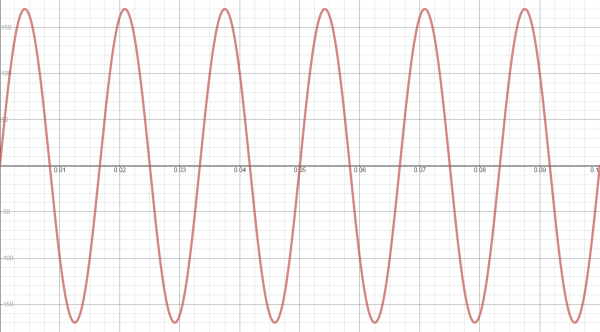
We can turn to our trusty outlet for a good example of how an AC waveform works. In the United States, the power provided to our homes is AC with about 170V zero-to-peak (amplitude) and 60Hz (frequency). We can plug these numbers into our formula to get the equation (remember that we are assuming our phase is 0):
We can use our handy graphing calculator to graph this equation. If no graphing calculator is available we can use a free online graphing program like Desmos (Note that you might have to use 'y' instead of 'v' in the equation to see the graph).
Notice that, as we predicted, the voltage rise up to 170V and down to -170V periodically. Additionally, 60 cycles of the sine wave occurs every second. If we were to measure the voltage in our outlets with an oscilloscope, this is what we would see (WARNING: do not attempt to measure the voltage in an outlet with an oscilloscope! This will likely damage the equipment).
NOTE: You might have heard that AC voltage in the US is 120V. This is also correct. How? When talking about AC (since the voltage changes constantly), it is often easier to use an average or mean. To accomplish that, we use a method called "Root mean squared." (RMS). It is often helpful to use the RMS value for AC when you want to calculate electrical power. Even though, in our example, we had the voltage varying from -170V to 170V, the root mean square is 120V RMS.
Applications
Home and office outlets are almost always AC. This is because generating and transporting AC across long distances is relatively easy. At high voltages (over 110kV), less energy is lost in electrical power transmission. Higher voltages mean lower currents, and lower currents mean less heat generated in the power line due to resistance. AC can be converted to and from high voltages easily using transformers.
AC is also capable of powering electric motors. Motors and generators are the exact same device, but motors convert electrical energy into mechanical energy (if the shaft on a motor is spun, a voltage is generated at the terminals!). This is useful for many large appliances like dishwashers, refrigerators, and so on, which run on AC.