Today was Meatball's birthday.

Turns out it's also Nick's birthday - you might know him from last week's AVC recap video. There are about 150 employees at SparkFun these days. What are the odds of this unexpected coincidence?
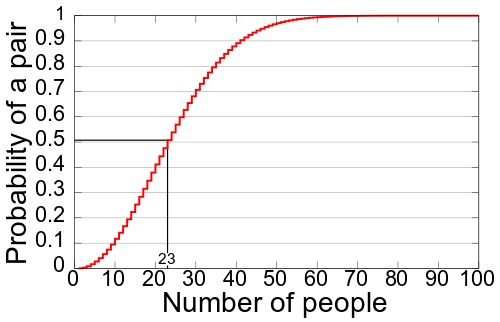
More generally: how many people, on average, do you need in a group before two people share the same birthday?
hint: it's not half of 365.
Believe-it-or-not answer: 23 people!
This famous problem in stats called the Birthday Paradox is a great example of how our intuition is often dead-stupid-wrong. It also involves nifty graphs like this:
After wishing happy birthday to Nick Meatball, I posed some follow-up riddles to the whole company:
Given the number of employees at SparkFun (about 150) how many pairs of birthdays should we statistically have? How many triplets?
How many do we actually have? It's not what you might expect...
18 pairs:
- Nick & Meatball
- Patrick & Erik
- Tim & Maya
- Ross & Bobby
- Juan & Ben
- Mike & Kyle
- Kim & Nick
- Rich & John
- Trevor & Gordon
- James & Jeff
- April & Paul
- Ben & Dav
- Jim & Patrick
- Mark & Mary
- Robert & Steven
- Brandon & Josh
- Destin & Chris
- Pete & Adam
And two triplets:
- Paul & Mike & Colin
- Abe & Jordan & Joe