Programming an FPGA

Sequential Logic and DFFs

Here is where things get really interesting. Combinational logic is very important but a system without any state or memory is pretty limited.

So how do you create memory? Essentially you just need some kind of feedback loop. If you want to create a counter, you simply add one to the result of the last addition.

The problem is, how do you control this loop? At first glance this may seem like a non-issue, but upon deeper inspection the Pandora's Box of issues become obvious.

Let’s take a look at the counter example.

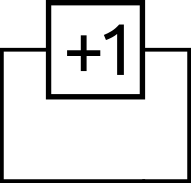
We could create it using an adder with one of the input values fixed at 1. I’ll wrap this up into a single block for simplicity. If we connect its input to the output we create an incrementing counter right?

Well, let me raise some questions. What value does this counter start at and how fast does it count?

The initial value would depend on how the power in the circuit was applied and how the circuit was laid out. It would also likely depend on the temperature and other environmental factors. You really don’t want your circuit to behave differently depending on the weather.

What’s worse is this circuit wouldn’t even work. This is because an addition circuit, like most combinational logic with multi-bit outputs, produces wrong intermediate results. In the case of an adder, the least-significant bit is calculated first with each following bit using the result of the previous bit in its calculations.

Since there is nothing waiting for the result to be valid, the wrong intermediate values are fed back into the adder which propagates more wrong values until the thing is just generating garbage.

So how do we fix this? We simply need a way to control the timing of the feedback loop. This is where DFFs, or D-type flip flops, are useful.

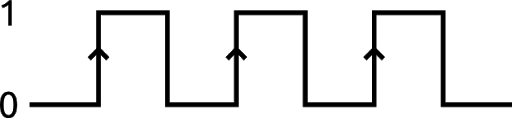
Before we dive into what exactly a DFF is, let me explain what a clock is. A clock is simply a signal that toggles from 0 to 1 over and over again at some set frequency.

The clock on the Alchitry boards toggles at 100MHz, or 100 million times a second. This regular signal can be used to give out circuits a sense of time.

The transition from 0 to 1 is known as the rising edge and is typically the important part of the signal. These edges are marked with arrows in the above image.

Back to the DFF.

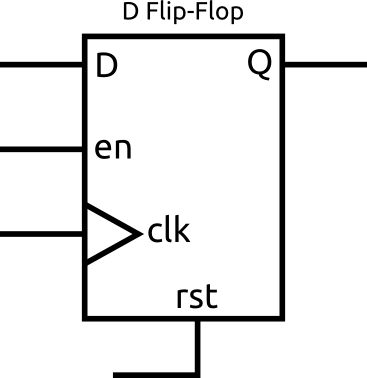
DFFs are a type of memory. They have an input, D, and an output, Q. When their clock input changes from 0 to 1, the value of D is saved and output on Q until the next rising edge of the clock.

It doesn’t matter if D changes between rising edges of the clock, the value on Q will stay the same.

In the above diagram, the DFF is shown with the optional enable and reset signals. The enable can be used to stop the DFF from copying in a new value on a rising edge. The reset signal is used to force the Q value to a known value. The DFFs in FPGAs can be configured to reset to 0 or 1.

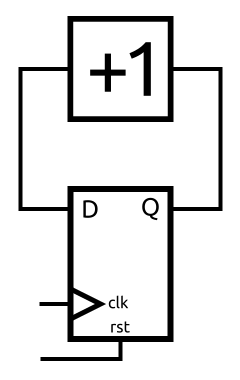
We can use the DFF in our counter to control the loop.

Now we can use the reset signal to set the initial value to something, for example 0. That means we know Q is 0. If Q is 0, then D will be 1.

On the rising edge of the clock, Q will get the value of D. That means Q becomes 1 and that means D becomes 2.

On each rising edge, Q will increment 1. This is exactly what we wanted!

The frequency of the clock determines how fast our counter will increment.

There are of course some restrictions on that. The clock needs to be slow enough so that the value at D has time to update after Q changes. We don’t want our DFF to save one of the invalid intermediate values that the adder produces.

The amount of time required for the adder’s output value to be valid is known as the propagation delay. This is the amount of time from a change of the inputs to the output being valid and stable.

The more logic you add, the longer this delay. The delay is also a function of the technology used to fabricate the circuit. The tools have models for each FPGA and if you tell it the clock frequency you are using, they will attempt to layout your design so that the timing requirements will be met.

In this example, we have one set of DFFs that is looping through a block of combinational logic. It is often more common to have the output of one set of DFFs fed through a block of combinational logic into another set of DFFs creating a pipeline.

In any design, the longest propagation delay sets the maximum frequency of the clock. By breaking up your design into roughly evenly timed blocks of combinational logic you can optimize the clock frequency.

The nitty gritty of timing can get pretty complicated but for most designs you can get away with using the same clock for the entire design and then the tools will simply take care of it as long as you don’t have any impossibly long paths. At 100MHz, you can actually do quite a lot between DFFs. It usually only becomes an issue if you attempt to chain too many things together or include a bunch of multiplication.

Meeting timing can also become difficult as you approach the resource limit in the FPGA. As the tools need to cram more and more into the same size FPGA they have reduced options for laying things out which can make them fail to meet timing requirements.