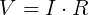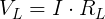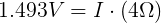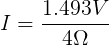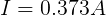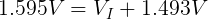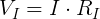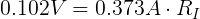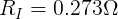Measuring Internal Resistance of Batteries
Internal Resistance
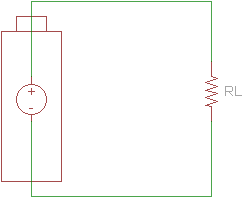
When designing a circuit with a battery, we often assume that the battery is an ideal voltage source. This means that no matter how much or little load we attach to the battery, the voltage at the source's terminals will always stay the same.
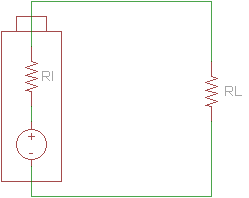
In reality, several factors can limit a battery's ability to act as an ideal voltage source. Battery size, chemical properties, age, and temperature all affect the amount of current a battery is able to source. As a result, we can create a better model of a battery with an ideal voltage source and a resistor in series.
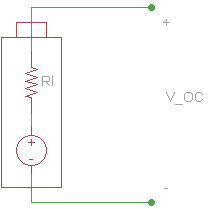
We can measure the voltage of a battery across its terminals without any load connected. This is known as the open-circuit voltage (VOC).
Note that because no current is flowing across the internal resistor, the voltage drop across it is 0 V. Therefore, we can assume that VOC is equal to the voltage of the ideal voltage source in the battery.
If we connect a load across the battery, the voltage across the terminals drops.
This drop in voltage is caused by the internal resistance of the battery. We can calculate the internal resistance if we take readings of the open-circuit voltage and the voltage across the battery's terminals with a load attached.
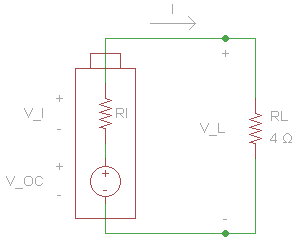
To start, we create a diagram showing our circuit.
We can plug in the loaded voltage we measured (VL) and the value of the resistor (RL) into Ohm's Law to get the current flowing through the circuit (I).
We also need to get the voltage across the internal resistor. We can do that using Kirchhoff's Voltage Law. Simplified for this circuit, we can say that the voltage drop across both resistors must add up to the voltage of the ideal voltage source.
Now that we know the voltage drop across the internal resistor and the current through it, we can use Ohm's Law again to find its resistance.
From this, we can see that the internal resistance (at this moment) of the AA cell is 0.273 Ω.