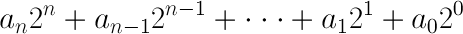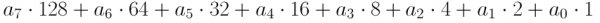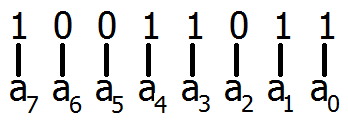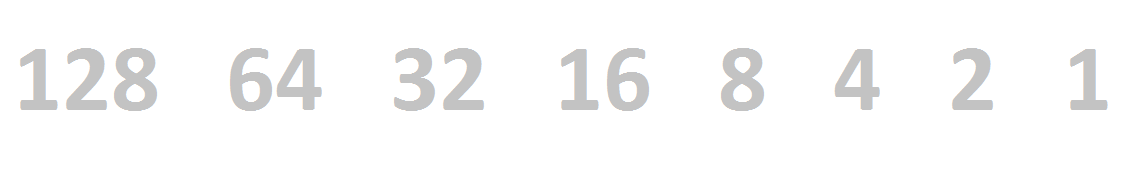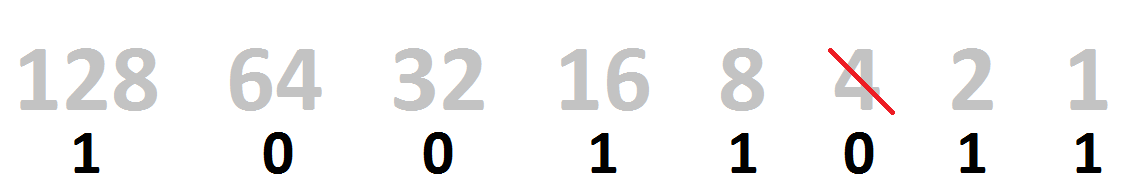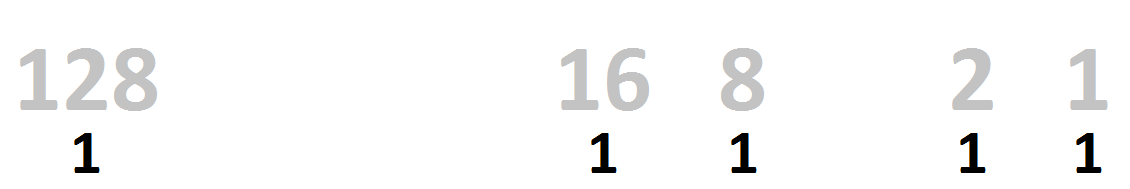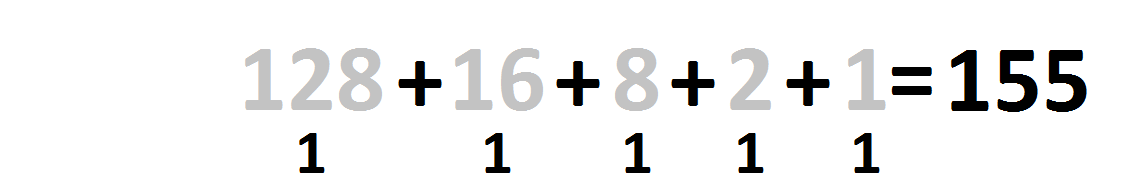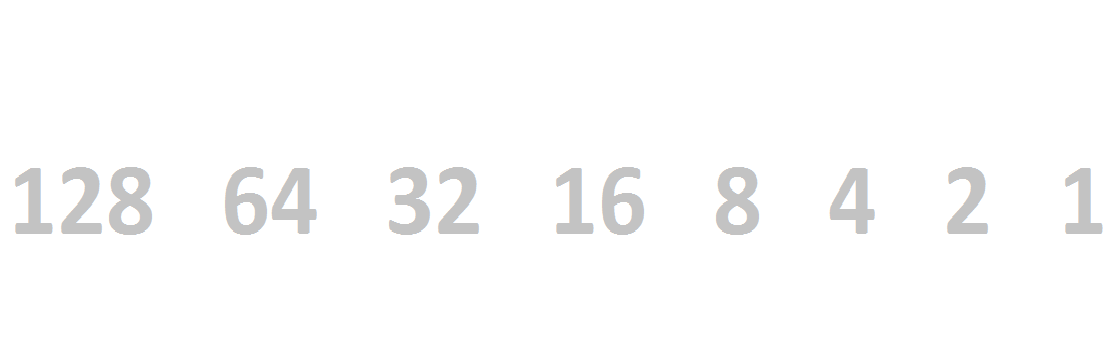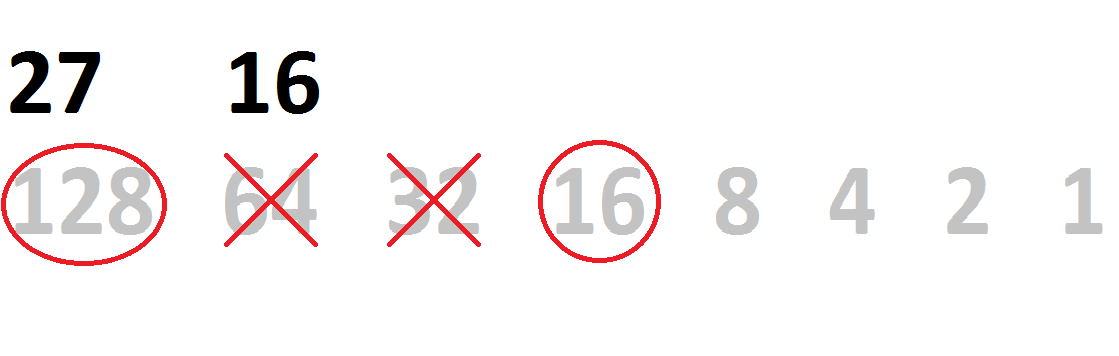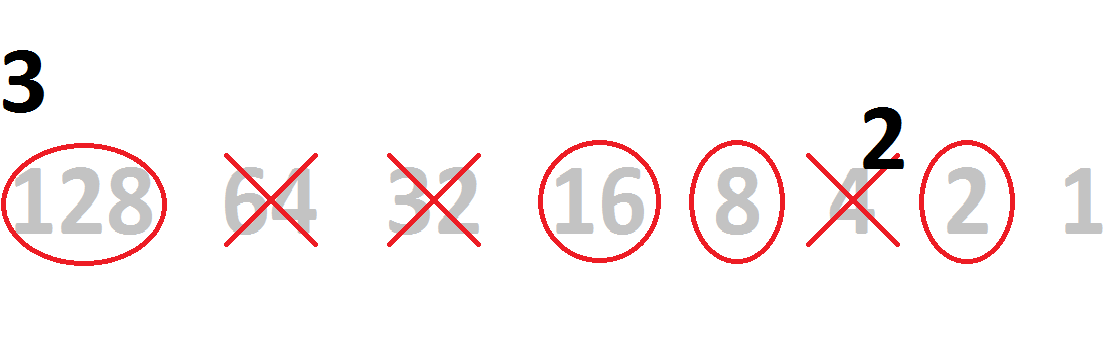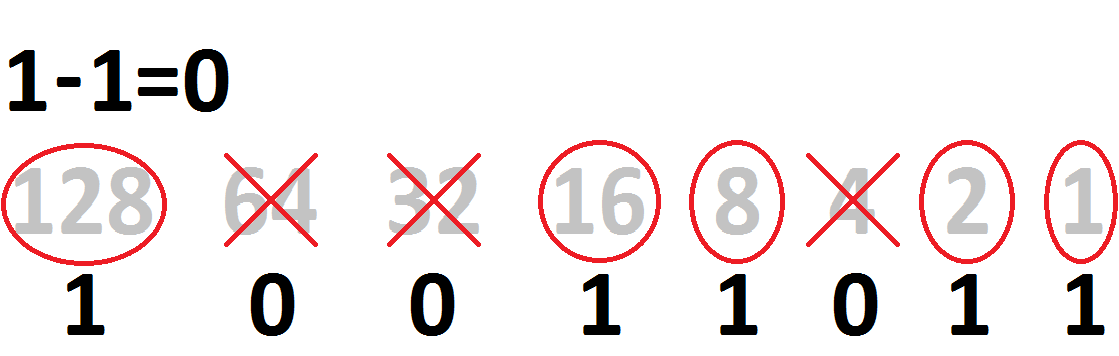Binary
Counting and Converting
The base of each number system is also called the radix. The radix of a decimal number is ten, and the radix of binary is two. The radix determines how many different symbols are required in order to flesh out a number system. In our decimal number system we’ve got 10 numeral representations for values between nothing and ten somethings: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Each of those symbols represents a very specific, standardized value.
In binary we’re only allowed two symbols: 0 and 1. But using those two symbols we can create any number that a decimal system can.
Counting in binary
You can count in decimal endlessly, even in your sleep, but how would you count in binary? Zero and one in base-two should look pretty familiar: 0 and 1. From there things get decidedly binary.
Remember that we’ve only got those two digits, so as we do in decimal, when we run out of symbols we’ve got to shift one column to the left, add a 1, and turn all of the digits to right to 0. So after 1 we get 10, then 11, then 100. Let’s start counting...
| Decimal | Binary | ... | Decimal | Binary |
| 0 | 0 | 16 | 10000 | |
| 1 | 1 | 17 | 10001 | |
| 2 | 10 | 18 | 10010 | |
| 3 | 11 | 19 | 10011 | |
| 4 | 100 | 20 | 10100 | |
| 5 | 101 | 21 | 10101 | |
| 6 | 110 | 22 | 10110 | |
| 7 | 111 | 23 | 10111 | |
| 8 | 1000 | 24 | 11000 | |
| 9 | 1001 | 25 | 11001 | |
| 10 | 1010 | 26 | 11010 | |
| 11 | 1011 | 27 | 11011 | |
| 12 | 1100 | 28 | 11100 | |
| 13 | 1101 | 29 | 11101 | |
| 14 | 1110 | 30 | 11110 | |
| 15 | 1111 | 31 | 11111 |
Does that start to paint the picture? Let’s examine how we might convert from those binary numbers to decimal.
Converting binary to decimal
There's no one way to convert binary-to-decimal. We'll outline two methods below, the more "mathy" method, and another that's more visual. We'll cover both, but if the first uses too much ugly terminology skip down to the second.
Method 1
There's a handy function we can use to convert any binary number to decimal:
There are four important elements to that equation:
- an, an-1, a1, etc., are the digits of a number. These are the 0's and 1's you're familiar with, but in binary they can only be 0 or 1.
- The position of a digit is also important to observe. The position starts at 0, on the right-most digit; this 1 or 0 is the least-significant. Every digit you move to the left increases in significance, and also increases the position by 1.
- The length of a binary number is given by the value of n, actually it's n+1. For example, a binary number like 101 has a length of 3, something larger, like 10011110 has a length of 8.
- Each digit is multiplied by a weight: the 2n, 2n-1, 21, etc. The right-most weight - 20 equates to 1, move one digit to the left and the weight becomes 2, then 4, 8, 16, 32, 64, 128, 256,... and on and on. Powers of two are of great importance to binary, they quickly become very familiar.
Let's get rid of those n's and exponents, and carry out our binary positional notation equation out eight positions:
Taking that further, let's plug in some values for the digits. What if you had a binary number like: 10011011? That would mean an values of:
For the sake of this tutorial, assume that the right-most value is always the least-significant. The least-significant digit in a number is the digit that has the smallest influence on a number’s ultimate value. The significance of the digits is arbitrary - part of a convention called endianness. A binary number can be either big-endian, where the most-significant digit is the left-most, or little-endian which we’ll use in this tutorial (and you’ll usually see binary numbers written this way).
Now, plug those digits into our binary to decimal equation. Because our number is little-endian the least-significant value should be multiplied by the smallest weight.
1 * 27 + 0 * 26 + 0 * 25 + 1 * 24 + 1 * 23 + 0 * 22 + 1 * 21 + 1 * 20And we can simplify it down to find our decimal number:
= 1 * 128 + 0 * 64 + 0 * 32 + 1 * 16 + 1 * 8 + 0 * 4 + 1 * 2 + 1 * 1
= 128 + 16 + 8 + 2 + 1
= 155
You’ll quickly notice that it takes many more digits to represent a number in binary than it does in decimal, but it’s all done with just two digits!
Method 2
Another, more visual way to convert binary numbers to decimal is to begin by sorting each 1 and 0 into a bin. Each bin has a successive power of two weight to it, the 1, 2, 4, 8, 16,... we’re used to. Carrying it out eight places would look something like this:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
So, if we sorted our 10011011 binary number into those bins, it’d look like this:
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
For every bin that has a binary 0 value in it, just cross out and remove it.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
And then add up any remaining weights to get your number!
Converting from decimal to binary
Just like going from binary to decimal, there's more than one way to convert decimal to binary. The first uses division and remainders, and the second uses subtraction. Try both, or stick to one you're comfortable with!
Method 1
It isn’t quite as simple to convert a decimal number to binary. This conversion requires repeatedly dividing the decimal number by 2, until you’ve reduced it to zero. Every time you divide the remainder of the division becomes a digit in the binary number you’re creating.
Don't remember how to do remainders? If it's been a while, remember that, since we're dividing by two, if the dividend is even, the remainder will be 0; an odd dividend means a remainder of 1.
For example, to convert 155 to binary you’d go through this process:
155 ÷ 2 = 77 R 1 (That’s the right-most digit, 1st position)
77 ÷ 2 = 38 R 1 (2nd position)
38 ÷ 2 = 19 R 0 (3rd position)
19 ÷ 2 = 9 R 1
9 ÷ 2 = 4 R 1
4 ÷ 2 = 2 R 0
2 ÷ 2 = 1 R 0
1 ÷ 2 = 0 R 1 (8th position)
The first remainder is the least-significant (right-most) digit, so read from top-to-bottom to flesh out our binary number right-to-left: 10011011. Match it up to the example above...that’s a bingo!
Method 2
If dividing and finding remainders isn’t your thing, there may be an easier method for converting decimal to binary. Start by finding the largest power of two that’s still smaller than your decimal number, and subtract it from the decimal. Then, continue to subtract by the largest possible power of two until you get to zero. Every weight-position that was subtracted, gets a binary 1 digit; digits that weren’t subtracted get a 0.
Continuing with our example, 155 can be subtracted by 128, producing 27:
| 155 - 128 = 27 | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | |||||||
Our new number, 27, can’t be subtracted by either 64 or 32. Both of those positions get a 0. We can subtract by 16, producing 11.
| 27 - 16 = 11 | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | ||||
And 8 subtracts from 11, producing 3. After that, no such luck with 4.
| 11 - 8 = 3 | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | ||
Our 3 can be subtracted by 2, producing 1. And finally, the 1 subtracts by 1 to make 0.
| 3 - 2 = 1 | |||||||
| 1 - 1 = 0 | |||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
We’ve got a binary number!
Conversion calculators
Fortunately, there are tons of binary-to-decimal and vice-versa calculators out there. You shouldn’t often need to resort to long-hand conversion.
Here! Plug some numbers into these boxes, and the other should magically change.
Make sure you only put 1's or 0's in the binary box, and 0-9 in the decimal one. Have fun!