Voltage, Current, Resistance, and Ohm's Law
Current
We can think of the amount of water flowing through the hose from the tank as current. The higher the pressure, the higher the flow, and vice-versa. With water, we would measure the volume of the water flowing through the hose over a certain period of time. With electricity, we measure the amount of charge flowing through the circuit over a period of time. Current is measured in Amperes (usually just referred to as "Amps"). An ampere is defined as 6.241*10^18 electrons (1 Coulomb) per second passing through a point in a circuit. Amps are represented in equations by the letter "I".
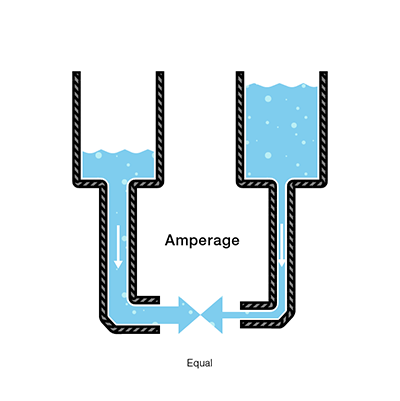
Let's say now that we have two tanks, each with a hose coming from the bottom. Each tank has the exact same amount of water, but the hose on one tank is narrower than the hose on the other.
We measure the same amount of pressure at the end of either hose, but when the water begins to flow, the flow rate of the water in the tank with the narrower hose will be less than the flow rate of the water in the tank with the wider hose. In electrical terms, the current through the narrower hose is less than the current through the wider hose. If we want the flow to be the same through both hoses, we have to increase the amount of water (charge) in the tank with the narrower hose.
This increases the pressure (voltage) at the end of the narrower hose, pushing more water through the tank. This is analogous to an increase in voltage that causes an increase in current.
Now we're starting to see the relationship between voltage and current. But there is a third factor to be considered here: the width of the hose. In this analogy, the width of the hose is the resistance. This means we need to add another term to our model:
- Water = Charge (measured in Coulombs)
- Pressure = Voltage (measured in Volts)
- Flow = Current (measured in Amperes, or "Amps" for short)
- Hose Width = Resistance