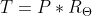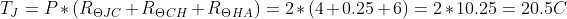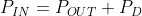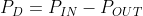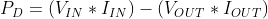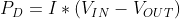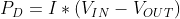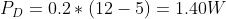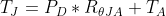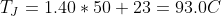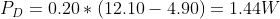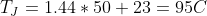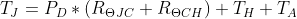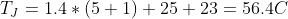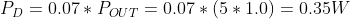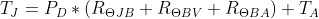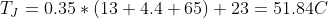Understanding Thermal Resistance

Introduction

When working with low power devices, thermal management isn’t much of an issue. Once you start adding motors, LED strips, and the current draw of the project goes up, parts can start to get hot. If you don’t manage the heat, parts can overheat, shortening the life of the component. In this tutorial we’ll cover what thermal resistance is, how it’s used for thermal management, and how to maximize the life of your project.

Suggested Reading

If you aren’t familiar with the following concepts, we recommend checking out these tutorials before continuing.

Thermal Resistance

To understand how power losses affect the heat generated, you first need to understand Thermal Resistance (R_θ). Similar to how electrical resistance resists the flow of current in ohms, thermal resistance resists the flow of heat in Kelvins per watt, or in degrees Celsius per watt. We can use thermal resistance to estimate how hot a particular part might get under various loads based on how easily the heat is able to be transfered from one place to another. For electronics the heat starts at the source, such as a semiconductor junction, and spreads to be eventually dissipated to ambient air.

If the junction of a semiconductor exceeds its maximum temperature it will break and let all the magic smoke out. To make sure we don't do that, we need to look at how efficiently the device is able to use the power.....

Ohm’s Law and Thermal Resistance

We can use ohm’s law to calculate the temperatures from the heatsink to the junction, and everywhere in between using Ohm’s Law. As mentioned earlier, electrical resistance is very similar to thermal resistance. We can use Ohm’s Law which states that V = I*R, and replace the voltage for temperature (T) and current for power (P), which gives us:

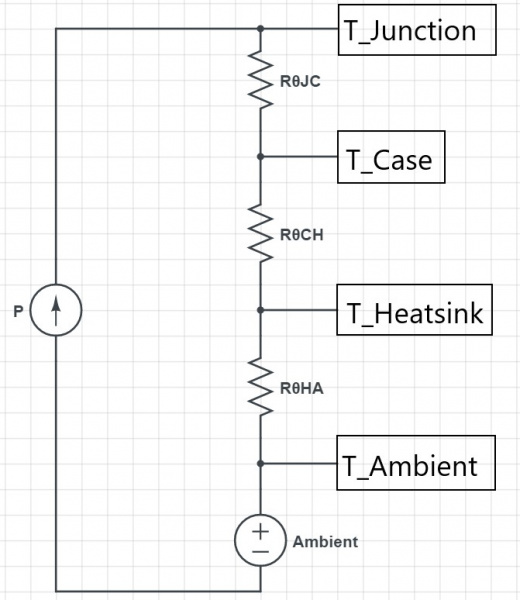
The equivalent thermal circuit is shown below where:

• T_Junction (T_J): the junction temperature
• R_θJC:the junction to case thermal resistance
• T_Case (T_C): the junction temperature
• R_θCH: the case to heatsink thermal resistance
• T_Heatsink (T_H): the heatsink temperature
• R_θHA: the heatsink to ambient air thermal resistance
• T_Ambient (T_A): the ambient air temperature

To better understand how thermal resistance is used, lets look at the following example:

• Power dissipated: 2W
• R_θJC = 4°C/W
• R_θCH = 0.25°C/W
• R_θHA = 6°C/W
• T_A = 25°C

Starting with the thermal equivalent of Ohm's Law:

We want to solve for our junction temperature rise , so T becomes T_J. Our power dissipated, P, is 2W. And our thermal resistances are in series, so just like resistors in series in a circuit we can add the values together:

The junction temperature is 20.5°C above ambient temperature (25°C in this case), which means the absolute temperature is 20.5°C + 25°C, which would be 45.5°C.

Where do you find the thermal resistance values? For parts like voltage regulators, diodes, transistors, and other semiconductors, the datasheet will have a section for the thermal information, mainly the Junction to Air (R_θJA) if some type of heatsink weren't used, or Junction to Case (R_θJC) if a heatsink was going to be used, which would have its own thermal resistance and is covered in the next section. The typical thermal resistance data would look similar to the image below.

How to Transfer Heat

Metal Fin Heatsinks

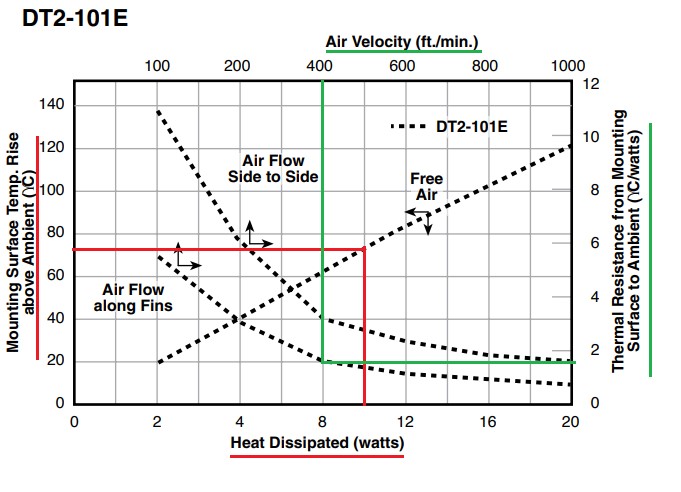
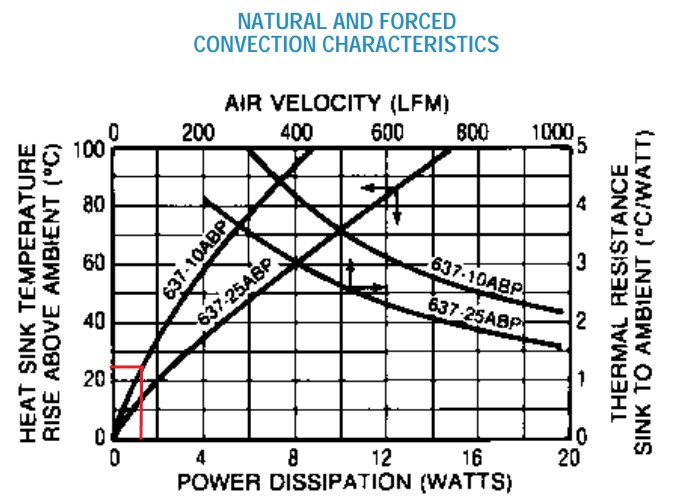
Heatsinks some in all shapes and sizes, with a single purpose: transfer heat to the air. The purpose of each of the fins on a heatsink is to create as much surface area as possible for the air to interact with and pull heat away from the heatsink, which helps to pull heat away from the semiconductor’s junction. The thermal resistance of a heatsink can be a bit complicated though because a metal fin heatsink performs at different rates based on the amount of air flowing past the fins. A typical datasheet for a heatsink provides not only the dimensions of the part, but the thermal characteristics as well, which looks like this:

The arrows on each plot line correspond to the axis they represent. For example, the red highlight shows that in free air (ie without a fan), dissipating 10W of power would raise the temperature of heatsink around 78°C above ambient temperature. If instead you had around 400ft/min of air flowing along the fins of the heatsink, the green line shows the heatsink would have a thermal resistance of around 1.8°C/W, or 18°C above ambient temperature dissipating the same 10W of power.

Vias

If you need to add a heatsink to the design, designs like switch mode power supplies where it’s important to keep components as close to the IC as possible, vias can not only transfer signals from one side of the PCB to the other, but they can transfer heat too!

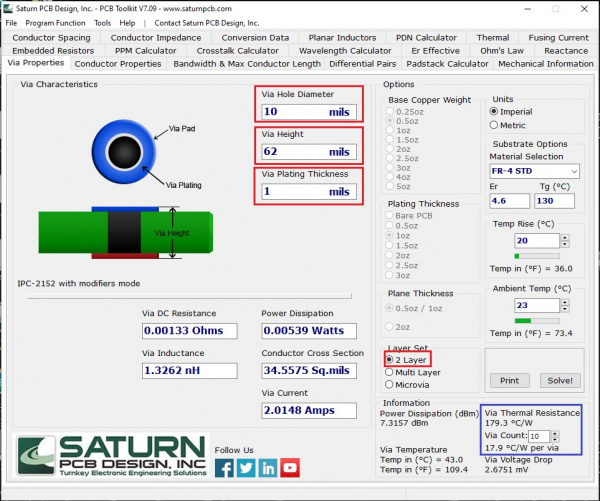
If you don’t feel like doing a bunch of math, the PCB Toolkit from Saturn PCB Design Inc has a lot of great tools to solve a ton of the equations an electrical engineer might use. One of the tabs in particular is for via properties:

To get the thermal resistance of the vias, I entered in the boxes I highlighted red the properties of the PCB I have. Setting the layer set to 2 layer, and the via hole diameter should be the only setting you might need to change. The via plating thickness and via height are pretty standard for most PCBs. After clicking solve, in the blue box in the bottom right corner I got the thermal resistance which was 179.3°C/W per via. With 10 vias, the via thermal resistance drops down to 17.9°C/W. If you were going to calculate the junction temperature now, you would add another thermal resistance in series for the vias, which would be added with the other thermal resistances when you do the calculation.

PCB Heatsinking

When it comes to transferring heat in a PCB, the math can get complicated pretty quickly, which is one of the reasons why for via thermal resistance, using the tool from Saturn PCB is the easier way to go. Even more complicated is using a PCB as a heatsink. There’s the thermal resistance not only of the copper, which is a function of the surface area, but the solder mask, substrate material, which also transfers heat to surrounding isolated copper planes. For a thorough explanation, you can read this application report from Texas Instruments. For easier to digest information, Paul Bryson has a great blog post on the subject and provides some great tips and findings which can be found here.

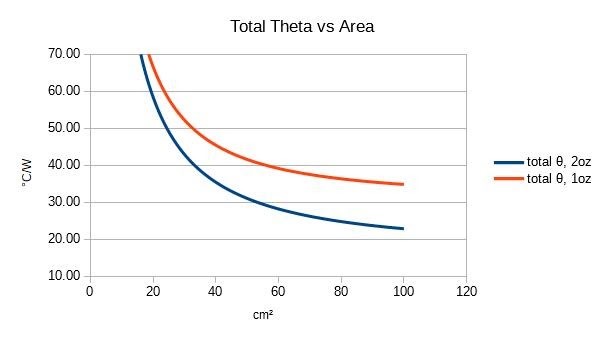
For a rough guide you can use the graph from Paul Bryson's post below:

Example: PTH Linear Regulator

Let’s see how well the thermal resistance calculations work in the real world. For these examples I’m going to use two different kinds of voltage regulators, a linear regulator, specifically the LM7805, as well as a DC-DC converter. We’ll see how well they stand up to the numbers we get from the datasheets.

Linear Regulator

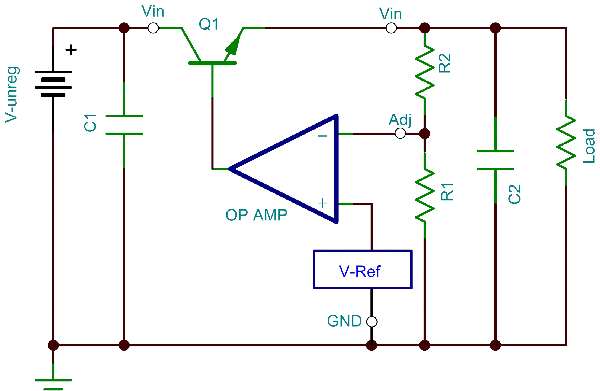
Having a low cost and low noise voltage regulator, how can you go wrong? Linear regulators are a great choice for many applications, but where they fall short is their efficiency. We can see the basic design of a linear regulator below:

To determine how hot a linear regulator will get, let’s start with the understanding that the input power must equal the output power. Ideally, the system would be 100% efficient, but in the real world there are going to be some losses, and that power loss is dissipated in the form of heat (P_D). This can be expressed as the following formula:

This means that the power dissipated can be expressed as:

In electronics power can be expressed as the product of the voltage and current. Which means we can rewrite the first equation as:

Now we need to look at the thermal characteristics of the linear regulator. The LM7805, has the following thermal resistances for the TO-220 package being used:

Without a heatsink (R_θJA)

For this first example, we’ll see how hot a linear regulator gets with only a 200mA load. TheLM7805 has an output voltage of 5V, and the input voltage will be around 12V. Plugging those numbers into our power loss equation from above, gives us:

To figure out how hot that will get without a heatsink, we’ll need to use the Junction to Air thermal resistance, which is 50°C/W. Using the formula from the thermal resistance section, and assuming ambient air temperature is 23°C, we can calculate the junction temperature to be:

To see how that compares to the real world, I measured the input voltage to be 12.1V and the output voltage under load to be 4.90V. I used a constant current dummy load set to 200mA connected to the output. Using the measured values, the dissipated power is:

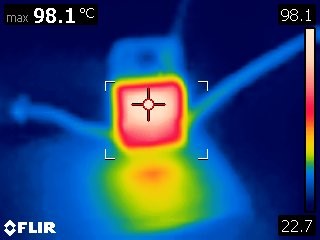
The expected junction temperature should then be:

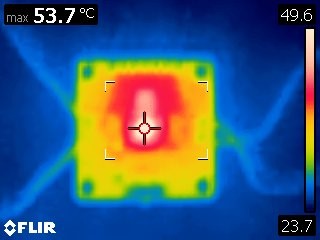
As the thermal image above shows, after turning on the load and letting the regulator heat up, it settled at a temperature of around 98°C. Pretty close, but it’s a good example of why it’s important to add margins to numbers. Due to the lack of precision, the power supply was slightly higher than we calculated, and under load, the regulator has a output voltage tolerance of 4%, which could allow the output voltage to drop to as low as 4.8V and still be in spec.

With a Heatsink (Using R_θJC)

Now with the addition of a heatsink, instead of using the thermal resistance from the junction to air, we need to use the value for junction to case, which is around 5°C/W. After looking at the datasheet for the heatsink I’m using, ~1.4W of power in free air would result in a 25°C temperature rise:

Because the heatsink provides a temperature rise instead of a thermal resistance, We will need to first calculate the junction temperature rise using the thermal resistance from the junction to the heatsink, and then add on temperature rise from the heatsink and ambient air temperature to get the junction temperature. Using thermal compound lowers the thermal resistance from the case to the heatsink (~0.25°C/W), without it we'll assume the thermal resistance is around 1°C/W. The junction temperature equation therefore becomes:

The actual voltages were the same as without a heatsink: Vin = 12.10V, Vout = 4.90V, Iout = 200mA. This resulted in the same 1.44W of power that actually needed to be dissipated, which only increased the calculated junction temperature to 56.64°C. After turning on power and enabling the load, I waited to let the temperature get up to a steady state temperature and measured the temperature of the regulator to be around 54°C.

This time the temperature was lower than we calculated. Most likely the error came from reading the temperature rise in still air for the heatsink, instead of 25°C, it could have been closer to 23°C. In the last example we’ll use a surface mount regulator and try to estimate how hot the regulator gets using the PCB as a heatsink.

Example: SMD DC/DC Converter

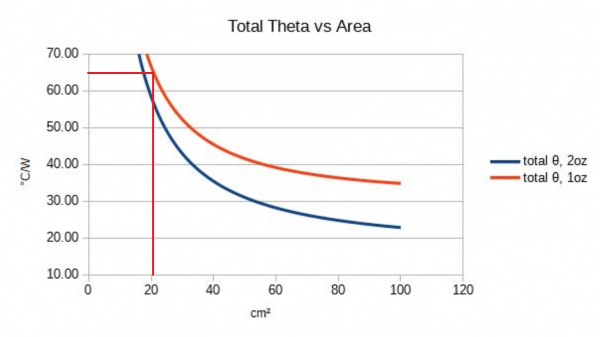
The board we’re using is the Buck-Boost, which uses the TPS63070 DC-DC converter. The board is 1.25x1.25 inches using 1oz copper. Other things to note, is the regulator is in the center of the board, and is over 95% solid copper. Because of the size, I’m going to make some assumptions by using the total board area for the thermal resistance, and use all 41 vias for the via thermal resistance.

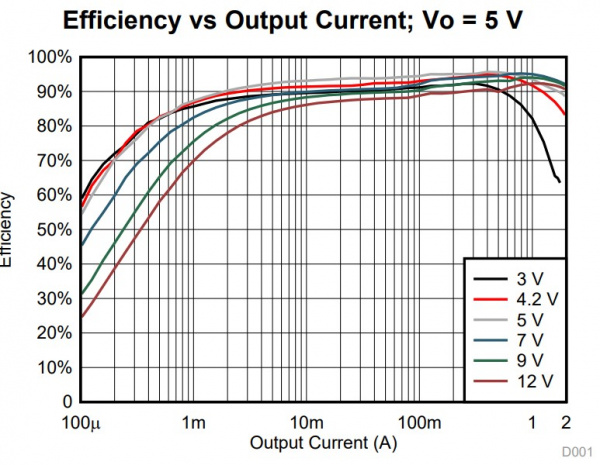
To get started we need to figure out how much power we need to dissipate. With a DC-DC converter, the input current does not equal the output current, so we can’t use the same formula as we did for the linear regulator. Instead we can estimate using the efficiency graph from the datasheet:

The efficiency graph plots the efficiency as a function of the output current, which is different based on the input and output voltages. For this test, we’ll use the same values before, having an input voltage of 12V and output voltage of 5V. This time though we’ll increase the load current to 1.0A. Using the 5V efficiency graph above, the efficiency should be around 93%, which would make our power loss 7% of the output power.

For the thermal resistances I used the via thermal resistance calculator and approximated the thermal resistance with the vias to be around 4.4°C/W using the values from the via calculation tool. To estimate the PCB thermal resistance, the board will be elevated off the table, to prevent using the table a heatsink. But because the bottom of the board is also in contact with the air, the surface area is now doubled from 10.08cm^2 to 20.16cm^2. Based on the surface area for the buck-boost board, I can estimate the PCBs thermal resistance to be around 65°C/W.

The datasheet for the TPS63070 has the following for the thermal characteristics:

The junction to case thermal resistance is not applicable, however the junction to board thermal resistance is, which is around 13°C/W. Using the thermal resistance values, we can plug that into the junction temperature equation:

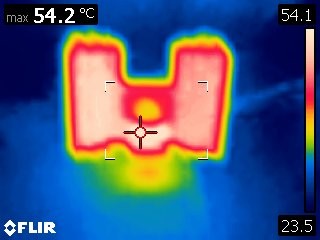
Just like before, I enabled the dummy load and let the board heat up until the temperature stopped rising. As shown below, I recorded a temperature of around 54°C.

Resources and Going Further

You can do these same calculations for a variety of power parts. For example you can look at the resistance between the drain and source of a mosfet to see how hot it might get at various currents. Or if you have a diode for reverse current protection, you can use the forward voltage drop and current. All these components will generate some amount of heat, but now you can take an educated guess as to how much.

Wanna use your new found skill set? Try out these great tutorials!