Programming an FPGA
Introduction
In this tutorial I’m going to cover the basics of what creating designs for an FPGA looks like and the fundamental building blocks you get to use. Let’s just get something cleared up real quick before we dive in. You don’t program FPGAs. It is often convenient to say we do just because it kind of feels like programming, you write some text, text is turned into a binary file, binary file is loaded on to the FPGA.
But you aren’t writing a program. You are creating a circuit. You don’t use programming languages to create circuits, you use hardware description languages (HDLs).
Large complex designs would get too complicated to draw out with a schematic so instead we describe the behavior we want in the circuit and the tools figure out how to actually implement it.
It’s important to keep in mind when creating designs for an FPGA that you are describing hardware and whatever you write will eventually end up as a physical circuit. It is possible to describe circuits that are impossible to implement or to describe something that seems simple but takes a huge amount of resources to implement.
Because of this, having a good idea of how the circuit you are trying to describe could be implemented is critical.
Required Materials
To follow along with this tutorial, you will need the following materials. You may not need everything though depending on what you have. Add it to your cart, read through the guide, and adjust the cart as necessary.
Suggested Reading
If you aren’t familiar with the following concepts, we recommend checking out these tutorials before continuing.
How Does an FPGA Work?
You may also want to check out some of Alchitry's tutorials. They can be found here:
- Excerpt from "Learning FPGAs: Digital Design for Beginners with Mojo and Lucid HDL"
- Alchitry Au+ Schematic (PDF)
- Alchitry Au Schematic (PDF)
- Alchitry Cu Schematic (PDF)
Structure of a Design
HDLs are typically based around the idea of a module. A module is a circuit block that has some number of inputs and outputs and contains some logic to glue them together. A module could contain sub-modules or it could be stand-alone; similar to how a program is broken down into functions.
While it would be possible to put an entire design into a single module, it is better practice to use smaller modules to perform each piece of your design. By breaking down your project into modules, you simplify the complexity of any one piece you need to work on at any given time. Some modules can be made to perform common tasks and are used over and over again.
When you start a design, it is often helpful to draw out a block diagram showing the various modules and how they connect to each other. This helps define the scope of your design and break it down logically.
It can be difficult to drastically change the flow of an entire design once you start writing it so the more planning that goes into the overall architecture before starting the better.
Lucid
For the rest of the tutorial, we will be using Lucid. Lucid is an HDL made specifically for FPGAs and is designed to remove many of the pitfalls that are common with other HDLs like Verilog and VHDL (and trust me, there are many).

Lucid is a fantastic place to begin working with FPGAs. I often am contacted by people who are worried about getting stuck using Lucid or want to just jump into Verilog or VHDL for some other reason. If you are just beginning, you should start with Lucid. It will teach you the proper fundamentals of hardware design before trying to fight your way through the cumbersome other HDLs.
If, down the road, you want to switch to something else, it isn’t very hard. Lucid is based roughly on Verilog and Alchitry Labs will actually convert Lucid to Verilog for you if you want to use your super snazzy modules somewhere else.
Without further ado, let’s jump into what makes up a module.
Anatomy of a Module
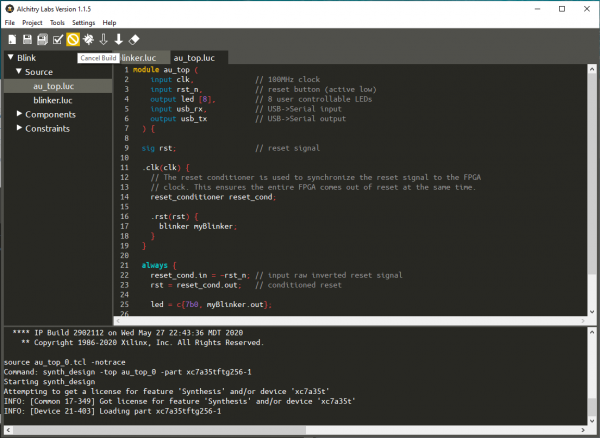
When you create any design, you will have a top-level module. This is the module whose inputs and outputs are actual inputs and outputs on the FPGA’s pins. For any Alchitry project, these are either cu_top.luc or au_top.luc depending on the board (Cu or Au) you are using.
The initial top-level modules for either board look essentially identical.
module au_top (
input clk, // 100MHz clock
input rst_n, // reset button (active low)
output led [8], // 8 user controllable LEDs
input usb_rx, // USB->Serial input
output usb_tx // USB->Serial output
) {
sig rst; // reset signal
.clk(clk) {
// The reset conditioner is used to synchronize the reset signal to the FPGA
// clock. This ensures the entire FPGA comes out of reset at the same time.
reset_conditioner reset_cond;
}
always {
reset_cond.in = ~rst_n; // input raw inverted reset signal
rst = reset_cond.out; // conditioned reset
led = 8h00; // turn LEDs off
usb_tx = usb_rx; // echo the serial data
}
}
Port Declarations
The first section of the module is the port declaration. This is where you declare the inputs and outputs to your module.
In this case, since it is the top-level module, these are signals on the board itself.
input clk, // 100MHz clock
input rst_n, // reset button (active low)
output led [8], // 8 user controllable LEDs
input usb_rx, // USB->Serial input
output usb_tx // USB->Serial output
You may have noticed the led input has a number in square brackets after it. This makes it not one, but eight individual inputs bound together as an array. We will get more into array syntax later.
A module may also have a list of parameters that can be used to customize the module. This list is omitted here and would be pointless on a top-level module since the parameters are passed in by the parent module instantiating it. The term instantiation is used to refer to when a module or other resource is added to your design. It means that an instance of that module or other resource is created.
When you write code, each time you call a function the exact same instructions are used over and over again no matter how many times the function is called. However, every time you instantiate a module, the entire circuit that composes the module is duplicated. If you want to reuse the same resources for multiple tasks, it is your job as the designer to figure out how you are going to juggle that.
Speaking of instantiation, typically you instantiate everything your module needs right after the port declaration.
The first line is declaring a signal using the sig keyword.
sig rst; // reset signal
Signals aren’t memory. They don’t store any values. You should think of them as wires. A wire can have a value, but it is really just a connection from one point to another.
In this design, we are using the signal rst as a placeholder for the output of the reset_conditioner module. Instantiating this module is what the next couple of lines do.
.clk(clk) {
// The reset conditioner is used to synchronize the reset signal to the FPGA
// clock. This ensures the entire FPGA comes out of reset at the same time.
reset_conditioner reset_cond;
}
To instantiate anything, you simply use the name of the resource followed by the name of this particular instance. So the line reset_conditioner reset_cond; creates an instance of the reset_conditioner module named reset_cond. The block that this instantiation is wrapped in is called a connection block. This block allows you to connect an input or parameter with a given name of many modules to the same signal.
In our case, we are connecting the input clk to the signal clk (which is an input to our module). The syntax is .port(signal) where port is the name of the input on the module being instantiated and signal is the signal to connect to it.
The reset_conditioner module has an input named clk so this input is directly connected to the signal clk in our module.
You could also connect this directly to the module on the line of instantiation like this:
reset_conditioner reset_cond(.clk(clk));
This wasn’t done here because the input clk is part of almost any module and it is convenient to have a block like this setup so you can simply add your other instantions that need to be connected to clk.
Almost every module will have a clk input and often they will have a rst input for a reset. Exactly what a clock and reset are used for will be covered later.
You can add multiple connections to the same connection block like this:
.clk(clk), .rst(rst) { … }
You can also nest the blocks and since not every block that uses clk uses rst - usually you will see something of the following form in the beginning of a module.
.clk(clk) {
// clk only instantiations
.rst(rst) {
// rst and clk instantiations
}
}
Always Blocks
The next section is the always block. This is the meat of the module.
Always blocks are where you describe all the logic that happens in your module. They contain something known as combinational logic. Combinational logic is any digital circuit whose output is a function solely of the current inputs. They have no internal state or memory. A good example of this is an addition circuit. The output is solely determined by the two numbers currently being input. It doesn’t matter what the last numbers input were or how many times you changed the numbers. The output is always a function of the current inputs.
Inside the always block we write statements. The statements are composed of four main types. Assignments, if statements, case statements, and for loops.
Assignments
Assignments are by far the most common. You have some signal on the left followed by an equals sign and then an expression.
signal = expression;
The power of these comes from the expression. Here you can use a handful of different operators to manipulate bits. These include some mathematical operators like +, -, and *. Notably, / for division can not be used if the expression is dynamic. This is because division is too complicated for the tools to have a reasonable default to drop in for you. Division is still possible, it just requires a bit more effort and planning.
If Statements
If statements follow your typical layout:
if (expr) { … } else { … }
If the expression following the if is true (non-zero) then the first set of lines are valid. If it is false (zero) the lines in the else block are valid. The else portion is optional.
Notice I said valid and not executed. It can be easy to fall into the trap when you have if statements and for loops to get in the programming mindset.
If statements are most often realized in hardware with a multiplexer. You are simply selecting one of two inputs based on some expression.
When you assign a signal a value in an always block, no matter what the conditions are, it must be assigned a value. This usually means that if you assign a value to something in an if statement you should have a matching assignment in the else portion of the statement.
The one exception to this rule is the d input of a dff or fsm type. These are covered later.
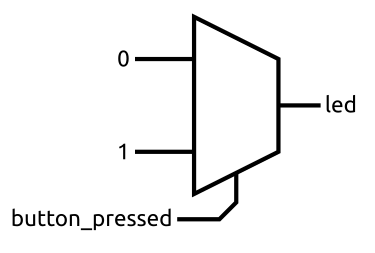
Another way to ensure you always assign a value is to begin your always block with some reasonable default values. Take a look at the following pseudo-code:
led = 0;
if (button_pressed)
led = 1;
When the button isn’t pressed, the led has the value 0. However, what happens when the button is pressed? Does led get assigned a value of 0 then updated with a value of 1? Nope.
When the button is pressed, led always has a value of 1. Assignments lower in an always block take precedence over previous assignments.
You can think of the block being evaluated always and instantaneously.
Now, imagine we didn’t have that default value before the if statement. What value would led have when the button isn’t pressed? It is tempting to assume that it would just keep its previous value but remember signals can’t store values. They are simply like wires connecting two things together.
With the default value of 0, we could realize this in hardware with a multiplexer.
In this trivial case, it could be simplified by just connecting the led and button_pressed signals together.
Case Statements
Case statements follow the following syntax:
case(expr) {
value: statement;
value: statement;
default: statement;
}
These work exactly the same as if statements but are just a simpler way to have many branches on a single expression. The value part of the case statement needs to be some constant. The optional default branch is a catch all.
Unlike with code, case statements don’t offer any performance improvements over many if statements. They are solely for code clarity and convenience.
For Loops
Finally we get to for loops. For loops in Lucid share the syntax to C or Java for loops but have some restrictions:
for (init; eval; increment) { … }
They are usually used with a var type which is used to store values that won’t directly show up in the circuit but are used in the description.
The big restriction on for loops in hardware is that they must have a constant number of iterations.
This is because the tools need to be able to unroll the loop. A for loop is no different than copy pasting that section of code over and over again except it is much easier to read. You should typically avoid them unless you have a good reason to use one. It is very easy to create a very large and slow circuit using for loops.
Numbers
In Lucid, there are a handful of ways to define a numeric constant. The easiest way is to simply type the number like 14.
When you see a lone number, it is in decimal (radix of 10) and the number of bits used to represent it are the minimum required in an unsigned format, unless it is negative.
If you want more control over the number of bits used, you can prefix the number with xd where x is the number of bits to be used. For example, 8d14 is the decimal value 14 represented with 8 bits.
You can trade out the d for h to use hexadecimal (radix of 16), or b for binary (radix of 2). With both of these formats you can specify the number of bits to use before the letter.
If you omit the number of bits, hexadecimal numbers default to using 4 bits per digit. For example, h08 uses 8 bits since I wrote two digits even though the value 8 could be represented with only 4 bits.
For binary, the number of bits is simply the number of digits when not explicitly specified. So, b101001 is six bits wide.
If a decimal number is written with the d but the number of bits omitted, it behaves the same as if the d was omitted as well.
Arrays
Many signals you will encounter will be multi-bit signals like the led input in our top-level module.
Bits in an array can be individually indexed using the syntax signal[bit] where bit is some expression. It is your job to ensure that the value will always fall within the bounds of the array if it is a dynamic value.
You can also access subsets of the bits using the array syntax [max:min]. Here the range of bits starting at min and going to max, inclusive, are selected. When using this syntax, both values need to be constants.
If you want to dynamically select a subset of bits you can use the syntax [start+:width]. Here start is the lowest bit to be selected and width is the number of bits to select above it (including the start bit). With this syntax, only width needs to be constant. You can also use the slight variation [start-:width]. With this syntax, start is the highest bit in the selection instead of the lowest.
Arrays in Lucid can be multi-dimensional. When declaring them you simply tack on some extra dimensions like this:
sig my_array[dim1][dim2][dim3];
All dimensions of an array must be declared with constant values.
You can then index the array using the selectors as before. Note that you can only use the sub-array selections as the last selector though.
Sequential Logic and DFFs
Here is where things get really interesting. Combinational logic is very important but a system without any state or memory is pretty limited.
So how do you create memory? Essentially you just need some kind of feedback loop. If you want to create a counter, you simply add one to the result of the last addition.
The problem is, how do you control this loop? At first glance this may seem like a non-issue, but upon deeper inspection the Pandora's Box of issues become obvious.
Let’s take a look at the counter example.
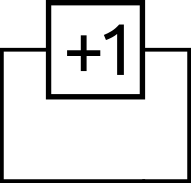
We could create it using an adder with one of the input values fixed at 1. I’ll wrap this up into a single block for simplicity. If we connect its input to the output we create an incrementing counter right?
Well, let me raise some questions. What value does this counter start at and how fast does it count?
The initial value would depend on how the power in the circuit was applied and how the circuit was laid out. It would also likely depend on the temperature and other environmental factors. You really don’t want your circuit to behave differently depending on the weather.
What’s worse is this circuit wouldn’t even work. This is because an addition circuit, like most combinational logic with multi-bit outputs, produces wrong intermediate results. In the case of an adder, the least-significant bit is calculated first with each following bit using the result of the previous bit in its calculations.
Since there is nothing waiting for the result to be valid, the wrong intermediate values are fed back into the adder which propagates more wrong values until the thing is just generating garbage.
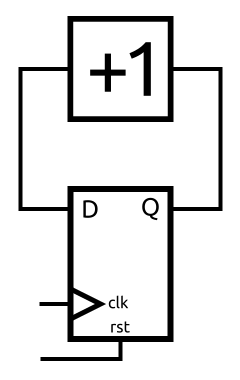
So how do we fix this? We simply need a way to control the timing of the feedback loop. This is where DFFs, or D-type flip flops, are useful.
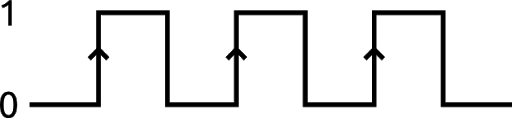
Before we dive into what exactly a DFF is, let me explain what a clock is. A clock is simply a signal that toggles from 0 to 1 over and over again at some set frequency.
The clock on the Alchitry boards toggles at 100MHz, or 100 million times a second. This regular signal can be used to give out circuits a sense of time.
The transition from 0 to 1 is known as the rising edge and is typically the important part of the signal. These edges are marked with arrows in the above image.
Back to the DFF.
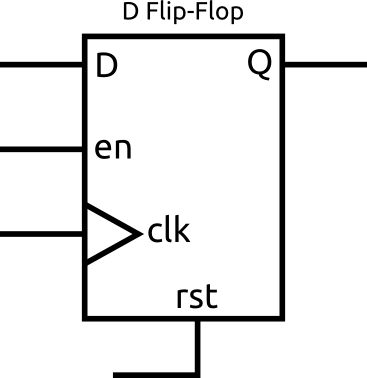
DFFs are a type of memory. They have an input, D, and an output, Q. When their clock input changes from 0 to 1, the value of D is saved and output on Q until the next rising edge of the clock.
It doesn’t matter if D changes between rising edges of the clock, the value on Q will stay the same.
In the above diagram, the DFF is shown with the optional enable and reset signals. The enable can be used to stop the DFF from copying in a new value on a rising edge. The reset signal is used to force the Q value to a known value. The DFFs in FPGAs can be configured to reset to 0 or 1.
We can use the DFF in our counter to control the loop.
Now we can use the reset signal to set the initial value to something, for example 0. That means we know Q is 0. If Q is 0, then D will be 1.
On the rising edge of the clock, Q will get the value of D. That means Q becomes 1 and that means D becomes 2.
On each rising edge, Q will increment 1. This is exactly what we wanted!
The frequency of the clock determines how fast our counter will increment.
There are of course some restrictions on that. The clock needs to be slow enough so that the value at D has time to update after Q changes. We don’t want our DFF to save one of the invalid intermediate values that the adder produces.
The amount of time required for the adder’s output value to be valid is known as the propagation delay. This is the amount of time from a change of the inputs to the output being valid and stable.
The more logic you add, the longer this delay. The delay is also a function of the technology used to fabricate the circuit. The tools have models for each FPGA and if you tell it the clock frequency you are using, they will attempt to layout your design so that the timing requirements will be met.
In this example, we have one set of DFFs that is looping through a block of combinational logic. It is often more common to have the output of one set of DFFs fed through a block of combinational logic into another set of DFFs creating a pipeline.
In any design, the longest propagation delay sets the maximum frequency of the clock. By breaking up your design into roughly evenly timed blocks of combinational logic you can optimize the clock frequency.
The nitty gritty of timing can get pretty complicated but for most designs you can get away with using the same clock for the entire design and then the tools will simply take care of it as long as you don’t have any impossibly long paths. At 100MHz, you can actually do quite a lot between DFFs. It usually only becomes an issue if you attempt to chain too many things together or include a bunch of multiplication.
Meeting timing can also become difficult as you approach the resource limit in the FPGA. As the tools need to cram more and more into the same size FPGA they have reduced options for laying things out which can make them fail to meet timing requirements.
Blink an LED
Let’s now put all this together into a demo project that will blink an LED.

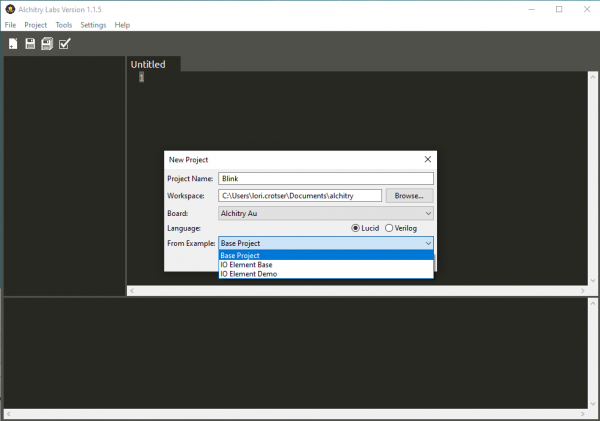
Create a New Project
Create a new project in Alchitry Labs and choose Base Project in the From Example dropdown.
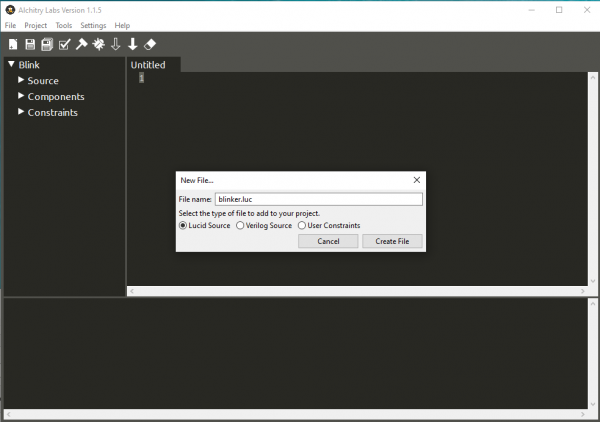
Click the new file icon in the toolbar (leftmost icon) and create a new Lucid Source file named blinker.luc.
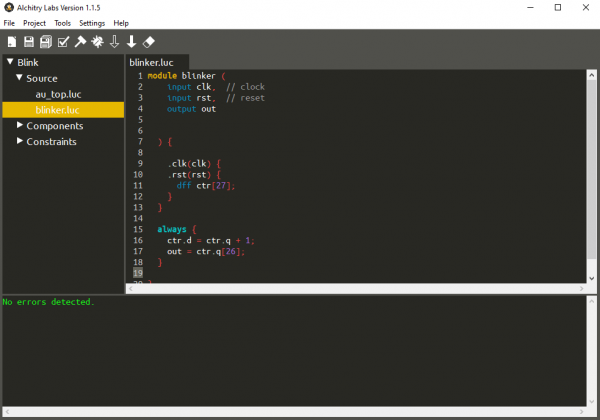
This will create a basic module that looks like the following:
module blinker (
input clk, // clock
input rst, // reset
output out
) {
always {
out = 0;
}
}
The default module template adds the clock and reset inputs and an output that currently does nothing.
To blink an LED we need to create a counter that will be used to toggle the LED. If we simply toggle the LED each clock cycle it will blink way too fast to be able to see.
We can set up the connection blocks for the clock and reset to make it easier then declare the DFF inside them.
.clk(clk) {
.rst(rst) {
dff ctr[27];
}
}
This creates an array of 27 DFFs named ctr. We can then hook up the DFF in the always block.
always {
ctr.d = ctr.q + 1;
out = ctr.q[26];
}
To access a module or DFFs signals, you use the dot notation. The first line of the always block connects the D input of the DFFs to the Q output plus 1. This will cause the value of ctr.q to increment once every clock cycle.
Note that the d signal is write-only and q is read-only.
The second line takes the most significant bit, number 26, and connects it to the output. Since ctr is 27 bits wide, it has indices from 0 to 26.
Since ctr will increment once per clock cycle, a 27 bit number can hold 2^27 = 134,217,728 different values, and our clock frequency is 100MHz, ctr will overflow once every 1.34 seconds.
For the first half of this cycle, the most significant bit will be 0. For the second half it will be 1. By connecting that bit to the output we will toggle the output every 0.67 seconds.
We can now head over to the top level module and instantiate our new module. Note that I’m using an Au, but the module would look the same for the Cu except the name would be cu_top instead of au_top.
module au_top (
input clk, // 100MHz clock
input rst_n, // reset button (active low)
output led [8], // 8 user controllable LEDs
input usb_rx, // USB->Serial input
output usb_tx // USB->Serial output
) {
sig rst; // reset signal
.clk(clk) {
// The reset conditioner is used to synchronize the reset signal to the FPGA
// clock. This ensures the entire FPGA comes out of reset at the same time.
reset_conditioner reset_cond;
.rst(rst) {
blinker myBlinker;
}
}
always {
reset_cond.in = ~rst_n; // input raw inverted reset signal
rst = reset_cond.out; // conditioned reset
led = c{7b0, myBlinker.out};
usb_tx = usb_rx; // echo the serial data
}
}
Here I added a connection block for the reset signal and created an instance of the blinker module named myBlinker.
Then, in the always block, I connected it to the led output using the concatenation syntax.
The elements inside c{...} get glued together to form a single array. So in our case, we are concatenating seven 0s with the bit from myBlinker.out. This will turn off the 7 most-significant LEDs and connect our blinker signal to the first LED.
You can now build the project by clicking on the hammer icon and then load it onto your board by pressing the solid down arrow icon.
The top LED should now be blinking slightly slower than once a second.
Module Improvements
We can improve our blinker module quite a bit to make it more useful.
First, the LED blinks with a bit of an awkward timing. We can make this exactly a second by counting to 50,000,000 and toggling the LED then.
To do this we need another DFF to store the state of the LED.
.clk(clk) {
.rst(rst) {
dff ctr[28];
dff led;
}
}
In the always block, we can now check to see if ctr.q is 49,999,999 (since 0 to 49,999,999 is 50,000,000 increments) and if it is we can reset it to 0 and toggle the LED.
always {
ctr.d = ctr.q + 1;
if (ctr.q == 49999999) {
ctr.d = 0;
led.d = ~led.q;
}
out = led.q;
}
Here I used the bit-wise inversion operator, ~. This inverts every bit of a signal. Since led.q is only one bit wide, it simply flips that bit.
If you remember from before, I said a signal needs to be assigned a value in all circumstances with the exception of DFFs. Since DFFs can actually save their value, if you don’t assign the d input during a clock cycle, the value of the DFF won’t change.
Our module now only stores the values of 0-49,999,999 in ctr but it is still a 28 bit array. This is wasteful as you only need 26 bits to store our values. We could simply change the array size to 26, but if we want to change the max value we would have to recompute this value each time.
Instead, we can use Lucid functions to calculate this for us. We can use $clog2(50000000) which will computer the ceiling log base 2 of the given value. This equates to “how many bits do I need to store this many combinations.” In our case, it’ll evaluate to 26.
dff ctr[$clog2(50000000)];
Speaking of changing the maximum value, we can edit our module to accept this as a parameter so it can be specified when the module is instantiated.
We can do this by adding a parameter list to our module. This comes before the port list.
module blinker #(
MAX_VALUE = 50000000 : MAX_VALUE > 0
)(
input clk, // clock
input rst, // reset
output out
) {
The port list is specified using the #(param, param, param) syntax. Each parameter can be as simple as just a name (in all capitals), or as complex as our example.
In our example, we set a default value of 50,000,000. Default values are typically a good idea unless you want to force a value to be specified at instantiation.
After the default assignment, you can specify a condition the parameter must meet. This condition can (and should) use the parameter itself as well as any parameters declared before it. This condition must evaluate to “true.” If it doesn’t, there will be an error reported when it is instantiated. This allows you to write your module with some assumptions about the parameter value and know that they will be obeyed.
We can then replace the occurrences of 50,000,000 in our module with MAX_VALUE.
module blinker #(
MAX_VALUE = 50000000 : MAX_VALUE > 0
)(
input clk, // clock
input rst, // reset
output out
) {
.clk(clk) {
.rst(rst) {
dff ctr[$clog2(MAX_VALUE)];
dff led;
}
}
always {
ctr.d = ctr.q + 1;
if (ctr.q == MAX_VALUE-1) {
ctr.d = 0;
led.d = ~led.q;
}
out = led.q;
}
}
If you build and load the project now, the LED should blink at a rate of once per second.
However, if you go back to the top-level module, you can change the instantiation to look like this.
blinker myBlinker(#MAX_VALUE(25000000));
Now if you build and load the project, the LED will blink twice per second.
In Summary
So there you have it. FPGA designs consist of blocks of combinational logic that do all the processing and DFFs that store values and control the flow of data.
The designs themselves are broken down into modules. Modules can be used by other modules and can even have parameters to customize each instantiation of them. Every time a module is instantiated, the circuit for it is duplicated in the FPGA.
When designing hardware, it is important to think about how that design could be implemented to create efficient circuits.
In the case of our blinker, if we didn’t care about the rate of blinking, the first version of the module would take a lot less resources to implement. This is because it doesn’t need a comparator to check the value of the counter. It simply keeps adding 1 and uses the natural overflow of binary addition to reset the counter.
Troubleshooting
If your product is not working as you expected or you need technical assistance or information, head on over to the Alchitry Forums. This is a great place to do some initial troubleshooting as well as to find and ask for help.

Resources and Going Further
Hopefully now you have a decent feel for what goes into creating a design for an FPGA. Alchitry's website has more great resources, including tutorials, projects, and the Alchitry Forum.
- Alchitry
- Alchitry Au+ Schematic (PDF)
- Alchitry Au Schematic (PDF)
- Alchitry Cu Schematic (PDF)
- Xilinx Artix 7 User Guide
If you'd like to delve deeper into the world of FPGAs and Lucid, check out "Learning FPGAs: Digital Design for Beginners with Mojo and Lucid HDL" by Justin Rajewski. It's available on Amazon and is a great resource for understanding and ultimately designing your own FPGAs.
We are continually expanding our offering of tutorials and products related to FPGAs. Check out some of the following tutorials!
How Does an FPGA Work?
First FPGA Project - Getting Fancy with PWM
External IO and Metastability