How Does an FPGA Work?
Look-Up Tables
So now that we have a way to dynamically route signals wherever they need to be, we need a way to perform arbitrary logic. We will again be using multiplexers, or rather a descendant of them known as LUTs or look-up tables.
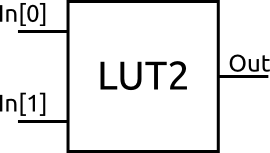
Imagine we have a multiplexer with four inputs and a 2 bit binary select (instead of one-hot). Now, instead of exposing the main inputs to the world, let’s hook them up to some programmable memory. This means we can program each input to some constant value. Wrap this all up into a block and we have a two input LUT.
The two inputs to the LUT are the select inputs of the multiplexer. By programming the multiplexer inputs to be whatever we want, we can use this LUT to implement ANY two-to-one binary function.
For example, we could make it act like a simple AND gate by setting the contents of the memory to be as follows.
| Address (In[1:0]) | Value (Out) |
|---|---|
| 00 | 0 |
| 01 | 0 |
| 10 | 0 |
| 11 | 1 |
This is a simple example - normally LUTs are bigger than just two inputs and the FPGA on the Alchitry Au is based around five input LUTs.
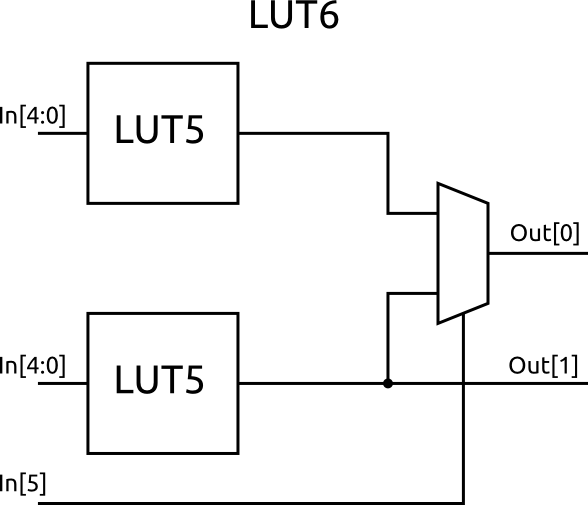
Xilinx actually puts two five input LUTs together with another multiplexer to create either a six input LUT or a five input LUT with two independent outputs.
If you want to really dive into what the LUTs and resources in the FPGA look like, check out this document from Xilinx on the Artix 7. This document is very dense. You’ve been warned. Page 20 is worth a glance though. It shows a simplified schematic of a SLICEL. Slices are one building-block above LUTs. The four boxes on the left are the LUTs like shown above.
For some context, the FPGA on the Alchitry Au has 20,800 dual LUTs. That’s a lot of LUTs but not even close to the largest FPGAs available which have about 260x that amount at the time of writing. As you can imagine, the routing of all those signals alone is insanely complex. Luckily for us, to use FPGAs you don’t need to do any of that. The tools take care of all the low level routing and LUT programming. We just get to describe the circuits we want.