Getting Started with Load Cells
Strain Gauge Basics
A strain gauge is a device that measures electrical resistance changes in response to, and proportional of, strain (or pressure or force or whatever you so desire to call it) applied to the device. The most common strain gauge is made up of very fine wire, or foil, set up in a grid pattern in such a way that there is a linear change in electrical resistance when strain is applied in one specific direction, most commonly found with a base resistance of 120Ω, 350Ω, and 1,000Ω.
Gauge Factor
Each strain gauge has a different sensitivity to strain, which is expressed quantitatively as the gauge factor (GF). The gauge factor is defined as the ratio of fractional change in electrical resistance to the fractional change in length (strain). (The gauge factor for metallic strain gauges is typically around 2.)
Small Changes in Strain
We set up a strain gauge load cell and measure that change in resistance and all is good, right? Not so fast. Strain measurements rarely involve quantities larger than a few millistrain (fancy units for strain, but still very small).
So lets take an example: suppose you put a strain of 500µε. A strain gauge with a gauge factor of 2 will have a change in electrical resistance of only:
For a 120Ω gauge, this is a change of only 0.12Ω. 0.12Ω is a very small change, and, for most devices, couldn't actually be detected, let alone detected accurately. So we are going to need another device that can either accurately measure super small changes in resistance (spoiler: they are very expensive) or a device that can take that very small change in resistance and turn it into something that we can measure accurately.
Amplifiers and Wheatstone Bridge
This is where an amplifier, such as the HX711 or the NAU7802 comes in handy.
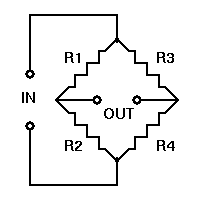
A good way of taking small changes in resistance and turning it into something more measurable is using a wheatstone bridge. A wheatstone bridge is a configuration of four resistors with a known voltage applied like this:
where Vin is a known constant voltage, and the resulting Vout is measured. If
,
then Vout is 0, but if there is a change to the value of one of the resistors, Vout will have a resulting change that can be measured and is governed by the following equation using Ohm's law:
By replacing one of the resistors in a wheatstone bridge with a strain gauge, we can easily measure the change in Vout and use that to assess the force applied.