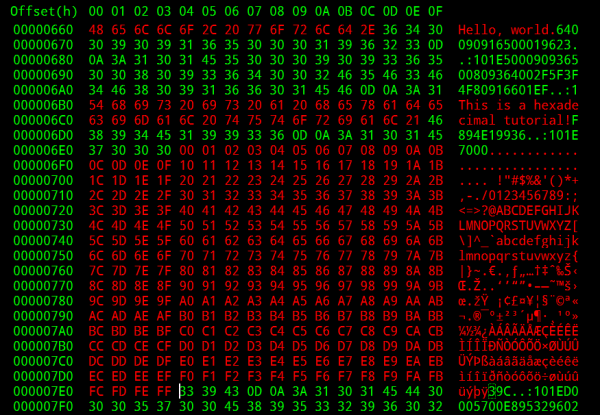
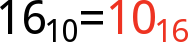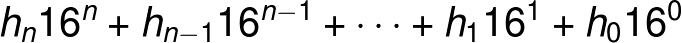Hexadecimal
Introduction
Have you ever felt constrained forming numbers with just 10 numerical digits? Or wanted to represent large numbers with fewer digits? Or easily identify byte values without having to look at binary's hypnotic string of 1's and 0's? For applications like these, hexadecimal often becomes the engineer's number-system-of-choice.
Hexadecimal -- also known as hex or base 16 -- is a system we can use to write and share numerical values. In that way it's no different than the most famous of numeral systems (the one we use every day): decimal. Decimal is a base 10 number system (perfect for beings with 10 fingers), and it uses a collection of 10 unique digits, which can be combined to positionally represent numbers.
Hex, like decimal, combines a set of digits to create large numbers. It just so happens that hex uses a set of 16 unique digits. Hex uses the standard 0-9, but it also incorporates six digits you wouldn't usually expect to see creating numbers: A, B, C, D, E, and F.
There are many (infinite!) other numeral systems out there. Binary (base 2) is also popular in the engineering world, because it's the language of computers. The base 2, binary, system uses just two digit values (0 and 1) to represent numbers.
Hex, along with decimal and binary, is one of the most commonly encountered numeral systems in the world of electronics and programming. It's important to understand how hex works, because, in many cases, it makes more sense to represent a number in base 16 than with binary or decimal.
Covered in This Tutorial
This tutorial covers everything hex-related that you might encounter in electronics or programming. It's split into the following sections:
- Hex Basics -- An overview of hex. This page covers the 16 digits of hex, how we represent hex numbers, and how to count in hex.
- Converting To/From Decimal -- This page covers our preferred methods of converting between hex and decimal.
- Converting To/From Binary -- This page shows how you can convert between binary and hex.
- Conversion Calculators -- Here you'll find a simple, automatic calculator to switch between hex, binary, and decimal.
Suggested Reading
You should know a thing or two about decimal numbers before delving into this tutorial. Remember long division? Remainders? Quotients? Products? Sums? Exponents? Those all come back to haunt you when you're learning about hexadecimal and its relationship to decimal.
Beyond brushing up on your arithmetic, we'd recommend reading through our binary tutorial before (or along-side) this.
Hex Basics
This page covers the very basics of hex, including an overview of the digits we use to represent hex numbers and tools we use to indicate a number is a hex value. We also cover very simple "decimal-to-hex" conversion in the form of hexadecimal counting.
The Digits: 0-9 and A-F
Hexadecimal is a base-16 number system. That means there are 16 possible digits used to represent numbers. 10 of the numerical values you're probably used to seeing in decimal numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9; those values still represent the same value you're used to. The remaining six digits are represented by A, B, C, D, E, and F, which map out to values of 10, 11, 12, 13, 14, and 15.
You'll probably encounter both upper and lower case representations of A-F. Both work. There isn't much of a standard in terms of upper versus lower case. A3F is the same number as a3f is the same number as A3f.
Subscripts
Decimal and hexadecimal have 10 digits in common, so they can create a lot of similar-looking numbers. But 10 in hex is a wholly different number from that in decimal. In fact hex 10 is equivalent to decimal 16. We need a way to explicitly state whether a number we're talking about is base 10 or base 16 (or base 8, or base 2). Enter base subscripts:
As you'll see further down, subscripts aren't the only way to explicitly state the base of a number. Subscripts are just the most literal system we can use.
Counting in Hex
Counting in hex is a lot like counting in decimal, except there are six more digits to deal with. Once a digit place becomes greater than "F", you roll that place over to "0", and increment the digit to the left by 1.
Let's do some counting:
| Decimal | Hexadecimal | ... | Decimal | Hexadecimal |
|---|---|---|---|---|
| 0 | 0 | 8 | 8 | |
| 1 | 1 | 9 | 9 | |
| 2 | 2 | 10 | A | |
| 3 | 3 | 11 | B | |
| 4 | 4 | 12 | C | |
| 5 | 5 | 13 | D | |
| 6 | 6 | 14 | E | |
| 7 | 7 | 15 | F |
Once you've reached F16, just as you would roll from 910 to 1010 in decimal, you roll up to 1016:
| Decimal | Hexadecimal | ... | Decimal | Hexadecimal |
|---|---|---|---|---|
| 16 | 10 | 24 | 18 | |
| 17 | 11 | 25 | 19 | |
| 18 | 12 | 26 | 1A | |
| 19 | 13 | 27 | 1B | |
| 20 | 14 | 28 | 1C | |
| 21 | 15 | 29 | 1D | |
| 22 | 16 | 30 | 1E | |
| 23 | 17 | 31 | 1F |
And once you've reached 1F16, roll up to 2016 and keep churning the right-most digit from 0 to F.
Hex Identifiers
"BEEF, it's what's for dinner". Am I channelling my inner Sam Elliott (McConaughey?), or expressing my hunger for the decimal number 48879? To avoid confusing situations like that, you'll usually see a hexadecimal number prefixed (or suffixed) with one of these identifiers:
| Identifier | Example | Notes |
|---|---|---|
| 0x | 0x47DE | This prefix shows up a lot in UNIX and C-based programming languages (like Arduino!). |
| # | #FF7734 | Color references in HTML and image editting programs. |
| % | %20 | Often used in URLs to express characters like "Space" (%20). |
| \x | \x0A | Often used to express character control codes like "Backspace" (\x08), "Escape" (\x1B), and "Line Feed" (\x0A). |
| &#x | Ω | Used in HTML, XML, and XHTML to express unicode characters (e.g. Ω prints an Ω). |
| 0h | 0h5E | A prefix used by many programmable graphic calculators (e.g. TI-89). |
| Numeral/Text Subscript | BE3716, 13Fhex | This is more of a mathematical represenatation of base 16 numbers. Decimal numbers can be represented with a subscript 10 (base 10). Binary is base 2. |
There are a variety of other prefixes and suffixes that are specific to certain programming languages. Assembly languagues, for example, might use an "H" or "h" suffix (e.g. 7Fh) or a "$" prefix ($6AD). Consult examples if you're not sure which prefix or suffix to use with your programming language.
The "0x" prefix is one you'll see a lot, especially if you're doing any Arduino programming. We'll use that from now on in this tutorial.
In summary: DECAF? A horrible abomination of coffee. 0xDECAF? A perfectly acceptable, 5-digit hexadecimal number.
Converting To/From Decimal
By now, we know how to convert about 16-or-so values between decimal and hexadecimal. To convert bigger numbers, here are some tricks we use.
Converting Decimal to Hex
Converting from decimal to hex involves a lot of division and remainders. If you've pushed long division out of your brain, wiki's always there to help you brush up.
The steps to convert a number, let's call it N, from decimal to hex look something like this:
- Divide N by 16. The remainder of that division is the first (least-significant/right-most) digit of your hex number. Take the quotient (the result of the division) to the next step.
- Note: if the remainder is 10, 11, 12, 13, 14, or 15, then that becomes the hex digit A, B, C, D, E, or F.
- Divide the quotient from the last step by 16 again. The remainder of this division is the second digit of your hex value (second-from-the-right). Take the quotient from this division to the next step.
- Divide the quotient from step 2 by 16 again. The remainder of this division is the third digit of your hex conversion. Noticing a pattern?
- Keep dividing your quotient from the last step by 16, and storing the remainder until the result of a division is 0. The remainder of that division is your hex value's left-most, most-significant digit.
Decimal-to-Hex Example: Convert 61453
Enough math-speak, let's work an example. Let's convert 6145310 to hexadecimal:
- Divide 61453 by 16. The result is a quotient of 3840, and a remainder of 13. That remainder becomes our first, right-most, least-significant hex digit -- D. Take 3840 to the next step.

- Now divide 3840 by 16. The resulting quotient is 240 with a remainder of 0. Our second hex digit is 0, and we take 240 to the next digit.

- Divide 240 by 16, and you'll get 15 with another 0 remainder. Our third hex digit is 0, and take 15 to step 4.
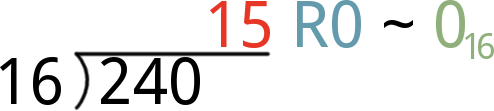
- Finally, divide 15 by 16. That'll produce the 0 quotient we've been waiting for, with a remainder of 15. That remainder means the hex digit for this position if F.
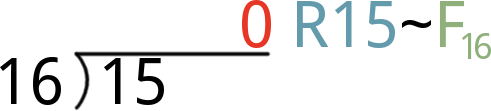
Finally, combine all four hex digits to create our hex value: 0xF00D.
Converting Hex to Decimal
There's an ugly equation that rules over hex-to-decimal conversion:
There are a few important elements to this equation. Each of the h factors (hn, hn-1) is a single digit of the hex value. If our hex value is 0xF00D, for example, h0 is D, h1 and h2 are 0, and h3 is F.
Powers of 16 are a critical part of hexadecimal. More-signficant digits (those towards the left side of the number) are multiplied by larger powers of 16. The least-significant digit, h0, is multiplied by 160 (1). If a hex value is four digits long, the most-significant digit is multiplied by 163, or 4096.
To convert a hexadecimal number to decimal, you need to plug in values for each of the h factors in the equation above. Then multiply each digit by its respective power of 16, and add each product up. Our step-by-step approach is:
- Start with the right-most digit of your hex value. Multiply it by 160, that is: multiply by 1. In other words, leave it be, but keep that value off to the side.
- Remember to convert alphabetic hex values (A, B, C, D, E, and F) to their decimal equivalent (10, 11, 12, 13, 14, and 15).
- Move one digit to the left. Multiply that digit by 161 (i.e. multipy by 16). Remember that product, and keep it to the side.
- Move another digit left. Multiply that digit by 162 (256) and store that product.
- Continue multiplying each incremental digit of the hex value by increasing powers of 16 (4096, 65536, 1048576, ...), and remember each product.
- Once you've multiplied each digit of the hex value by the proper power of 16, add them all up. That sum is the decimal equivalent of your hex value.
Hex-to-Decimal Example: Convert 0xC0DE
Here's an example of a four-digit hexadecimal value, 0xC0DE, that we want to convert to decimal. Creating a table and sorting the digits into separate columns can make the conversion process easier:
| Hexadecimal Digit | Notes | ||||
|---|---|---|---|---|---|
| Digit Positions (n) | 3 | 2 | 1 | 0 | These values are statically assigned, they grow to the left. |
| Hex Digits Sorted | C | 0 | D | E | This part's easy, plug your hex values in from right-to-left. |
| Convert A-F | 12 | 0 | 13 | 14 | Convert hex values A-F to 10-15. |
| Multiply by 16n | 12 × 163 | 0 × 162 | 13 × 161 | 14 × 160 | The exponent of 16 is the position, n. |
| Resulting Products | 49152 | 0 | 208 | 14 | The product of hex digit and the power of 16. |
| Sum Up All Products | 49374 | Our decimal equivalent! | |||
There you have it. CODE16 = 4937410!
This table method is perfect for keeping all of your hex digits, positions, and powers-of-16 in line. To convert larger hex numbers, just add a columns to the left and increase n.
Now that you know how to do it by hand, save yourself a little time and use a calculator.
Converting To/From Binary
Breathe easy! We've gotten the hard conversions out of the way. We use hex in electrical and computer engineering because it's incredibly easy to convert to and from binary -- the 1's and 0's language of computers.
Converting between hex and binary is easy, because each digit of a hexadecimal number "maps" to four bits (a bit being an individual binary digit) of a binary value. So a byte -- eight binary digits -- can always be represented by two hexadecimal digits. This makes hex a really great, concise way to represent a byte or group of bytes.
Converting from Binary to Hex
Let's begin by mapping the first 16 hexadecimal values to binary.
| Decimal | Hex | Binary | ... | Decimal | Hex | Binary |
|---|---|---|---|---|---|---|
| 00 | 0 | 0000 | 08 | 8 | 1000 | |
| 01 | 1 | 0001 | 09 | 9 | 1001 | |
| 02 | 2 | 0010 | 10 | A | 1010 | |
| 03 | 3 | 0011 | 11 | B | 1011 | |
| 04 | 4 | 0100 | 12 | C | 1100 | |
| 05 | 5 | 0101 | 13 | D | 1101 | |
| 06 | 6 | 0110 | 14 | E | 1110 | |
| 07 | 7 | 0111 | 15 | F | 1111 |
As you grow, and continue to use hex and binary, these 16 values will become ingrained in your brain. Those are the key to converting between hex and binary.
To convert between binary and hex, we want to take advantage of the fact that four binary digits (bits) map to one hex digit. Follow these steps to convert from binary to hex.
- Split a binary value into groups of four, starting at the right-most side.
- For each group of four, consult the table above to find the matching hex value, and replace groups of four binary digits with the one hex value.
That's it! Let's try it out.
Binary to Hex Example: Convert 0b101111010100001
To begin, start at the far-right of the binary number, and sort the 1's and 0's into groups of four:
| Binary Digits Sorted: | 0101 | 1110 | 1010 | 0001 |
|---|
Now consult our big table-o'-sixteen to convert the groups-of-four to a hex digit:
| Binary Digits Sorted: | 0101 | 1110 | 1010 | 0001 |
|---|---|---|---|---|
| Hex Equivalents: | 5 | E | A | 1 |
And there you have it! 0b101111010100001 = 0x5EA1. (Ugh. This tutorial has far exceeded everyone's tolerance for 1337. My apologies.)
Converting from Hex to Binary
Converting from hex to binary is a lot like converting binary to hex. Simply take a hex digit and turn it into four binary digits. Repeat until your number is full of 0's and 1's.
Hex to Binary Example: Convert 0xDEADBEEF
To convert 0xDEADBEEF (a commonly used code to indicate a system crash), begin by sorting the digits into "bins":
| Hex Digits Sorted: | D | E | A | D | B | E | E | F |
|---|
Then convert each hex digit into four bits:
| Hex Digits Sorted: | D | E | A | D | B | E | E | F |
|---|---|---|---|---|---|---|---|---|
| Hex Digits Sorted: | 1101 | 1110 | 1010 | 1101 | 1011 | 1110 | 1110 | 1111 |
In other words, 0xDEADBEEF = 0b11011110101011011011111011101111. That's a lot of 1's and 0's.
Use Hex to Represent and Identify Bytes
The examples above show off one of hex's greatest powers: easily representing values of bytes. Hex is often easier for us to work with because the values are shorter and more memorable than a long string of 1's and 0's.
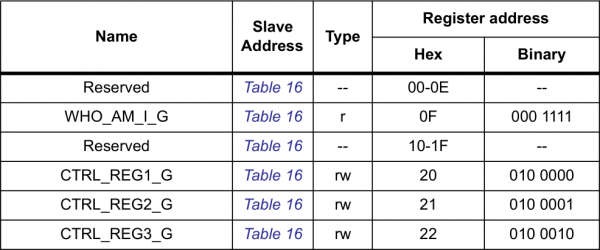
For example, the register map above is from the LSM9DS0 (a nifty, 9DOF sensor). It lists register addresses, which are used to control the sensor, in both hex and binary. If you want to access the CTRL_REG2_G register, it's much easier to remember 0x21 than 0b010001, and discovering a typo in the hex value is much easier than in binary. For that reason, we're much more likely to use hex values in our code than their binary equivalents.
Conversion Calculators
If you're overdosing on long division, trying to convert decimal to hexadecimal, or getting lost trying to calculate powers of 16, give these calculators a try.
Entering a number into any of the boxes below will automatically update the others with the matching value. You can type a hex value in, to convert to binary and decimal. Or type a decimal or binary number to generate a hex value. Use it as you please!
This calculator requires Javascript. If it isn't working, make sure JS is enabled (if'n you please).
Resources and Going Further
Understanding how hexadecimal works is key to so many areas of electronics and programming.
Armed with your shiny, new hex knowledge, here are some related tutorials you may want to check out from here:
- Digital Logic and Shift registers -- These tutorials use hex as a foundation for larger, more general electronics concepts. Digital logic is the core behind all of the decision making a computer does. Shift registers can be used to fan a single input or output out to 8-or-more.
- I2C and SPI -- These communication interfaces almost always require use of hex in some way or another. Devices that communicate of SPI or I2C usually have a list of registers, which are all mapped with hexadecimal addresses. I2C devices are all assigned unique, 7-bit addresses, which are usually presented in hexadecimal.
- Binary Blaster Hookup Guide -- If you're looking to practice your hex conversions, the Binary Blaster Kit can be a great help. This is a soldering kit. Once you've put it together, use it to test your knowledge of how binary, hex, and decimal are related.